题目内容
8.某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.表1
| 生产能力分组 | 人数 |
| [100,110) | 4 |
| [110,120) | 8 |
| [120,130) | x |
| [130,140) | 5 |
| [140,150) | 3 |
| 生产能力分组 | 人数 |
| [110,120) | 6 |
| [120,130) | y |
| [130,140) | 36 |
| [140,150) | 18 |
(2)估计A类工人生产能力的平均数.(同一组中的数据用该组区间的中点值作代表)
分析 (1)根据分层抽样的特征是各层所抽取的样本数比例相等,计算出A、B类工人应抽查的人数,根据样本容量计算出x、y的值并补充完整频率分布直方图;
(2)计算出样本中A类工人生产能力的平均数,并由此估计该工厂A类工人的生产能力的平均数即可.
解答 解:(1)由题意知,A类工人中应抽查25名,B类工人中应抽查75名. …(1分)
故4+8+x+5+3=25,得x=5,6+y+36+18=75,得y=15.…(3分)
频率分布直方图如图:…(11分)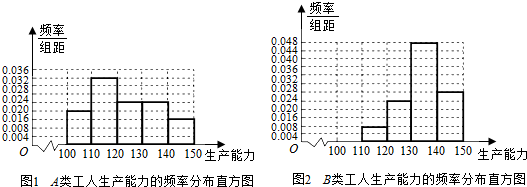
(2)$\overline{XA}$=$\frac{4}{25}$×105+$\frac{8}{25}$×115+$\frac{5}{25}$×125+$\frac{5}{25}$×135+$\frac{3}{25}$×145=123,…(11分)
∴A类工人生产能力平均数的估计值为123.…(14分)
点评 本题考查了频率分布直方图以及求数据的平均数的问题,解题时应熟练地掌握这些知识并能灵活应用,是基础题.

练习册系列答案
相关题目
2.已知平面α,β和直线a,b,若α∩β=l,a?α,b?β,且平面与平面β不垂直,直线a与直线l不垂直,直线b与直线l不垂直,则( )
| A. | 直线a与直线b可能垂直,但不可能平行 | |
| B. | 直线a与直线b可能垂直,也可能平行 | |
| C. | 直线a与直线b不可能垂直,但可能平行 | |
| D. | 直线a与直线b不可能垂直,也不可能平行 |
16.若平面α的一个法向量$\overrightarrow n$=(2,1,1),直线l的一个方向向量为$\overrightarrow a$=(1,2,3),则l与α所成角的正弦值为( )
| A. | $\frac{\sqrt{17}}{6}$ | B. | $\frac{\sqrt{21}}{6}$ | C. | -$\frac{\sqrt{21}}{6}$ | D. | $\frac{\sqrt{21}}{3}$ |
3.在研究色盲与性别的关系调查中,调查了男性400人,其中有30人患色盲,调查的600名女性中有20人患色盲.
(1)根据以上数据建立一个2×2列联表;
(2)有多大把握认为“性别与患色盲有关系”?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
附临界值参考表:
(1)根据以上数据建立一个2×2列联表;
(2)有多大把握认为“性别与患色盲有关系”?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)•g(x)+f(x)•g′(x)>0,且f(-3)•g(-3)=0,则不等式f(x)•g(x)<0的解集是( )
| A. | (-3,0)∪(3,+∞) | B. | (-3,0)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-∞,-3)∪(0,3) |
20.设θ是第三象限角,且|cos$\frac{θ}{2}$|=-cos$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
17.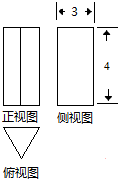 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
 如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )
如图,一个几何体的三视图,侧视图和正视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的体积为( )| A. | 18 | B. | 9$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
18.设i是虚数单位,则复数$\frac{4+3i}{3-4i}$=( )
| A. | $\frac{4}{5}+\frac{3}{5}i$ | B. | $\frac{4}{25}+\frac{3}{25}i$ | C. | -i | D. | i |