题目内容
17．
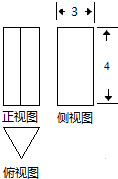如图，一个几何体的三视图，侧视图和正视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的体积为（ ）| A． | 18 | B． | 9$\sqrt{3}$ | C． | 12$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
分析 根据几何体的三视图，得出该几何体是底面为等边三角形，高为4的直三棱柱，求出它的体积即可．
解答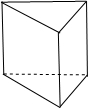 
解：根据几何体的三视图，得
该几何体是如图所示的直三棱柱；
且该三棱柱的底面边长上的高为3的等边三角形；
所以，该三棱柱的底面边长为a=$\frac{3}{si{n60}^{°}}$=2$\sqrt{3}$，
它的体积为：
V=Sh=$\frac{1}{2}$×2$\sqrt{3}$×3×4=12$\sqrt{3}$．
故选：C．
点评 本题考查了空间几何体的三视图的应用问题，解题时应根据三视图得出几何体的直观图，是基础题目．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
7．
从4种不同的颜色中选择若干种给如图所示的4个方格涂色，每个方格中只涂一种颜色且相邻两格不能涂同一种颜色，则不同的涂色方法共有（ ）
从4种不同的颜色中选择若干种给如图所示的4个方格涂色，每个方格中只涂一种颜色且相邻两格不能涂同一种颜色，则不同的涂色方法共有（ ）| A． | 24种 | B． | 72种 | C． | 96种 | D． | 108种 |
8．某工厂有工人1000名，其中250名工人参加过短期培训（称为A类工人），另外750名工人参加过长期培训（称为B类工人），现用分层抽样方法（按A类、B类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（此处生产能力指一天加工的零件数）．从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2．
表1
表2
（1）先确定x，y，再完成下列频率分布直方图．
（2）估计A类工人生产能力的平均数．（同一组中的数据用该组区间的中点值作代表）
表1
| 生产能力分组 | 人数 |
| [100，110） | 4 |
| [110，120） | 8 |
| [120，130） | x |
| [130，140） | 5 |
| [140，150） | 3 |
| 生产能力分组 | 人数 |
| [110，120） | 6 |
| [120，130） | y |
| [130，140） | 36 |
| [140，150） | 18 |
（2）估计A类工人生产能力的平均数．（同一组中的数据用该组区间的中点值作代表）
9．四个小动物换座位，开始是猴、兔、猫、鼠分别坐在1、2、3、4号位置上（如图），第1次前后排动物互换位置，第2次左右列互换座位，…这样交替进行下去，那么第2014次互换座位后，小兔的位置对应的是（ ）
| A． | 编号1 （开始） | B． | 编号2 （第1次） | C． | 编号3 （第2次） | D． | 编号4（第3次） |