题目内容
3.在研究色盲与性别的关系调查中,调查了男性400人,其中有30人患色盲,调查的600名女性中有20人患色盲.(1)根据以上数据建立一个2×2列联表;
(2)有多大把握认为“性别与患色盲有关系”?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲,列出列联表;
(2)代入公式计算得出K2值,结合临界值,即可求得结论.
解答 解:(1)性别与色盲的2×2列联表建立如下:
| 患色盲 | 不患色盲 | 总计 | |
| 男 | 30 | 370 | 400 |
| 女 | 20 | 580 | 600 |
| 总计 | 50 | 950 | 1 000 |
(2)假设H0:“性别与患色盲没有关系”,根据(1)中2×2列联表中数据,可求得${K^2}={\frac{{1000({30×580-20×370})}}{50×950×400×600}^2}≈8.772$…(8分)
又P(K2≥7.879)=0.005,即H0成立的概率不超过0.005,…(10分)
故若认为“性别与患色盲有关系”,则出错的概率不超过0.005.
所以有99.5%的把握认为“性别与患色盲有关系”…(12分).
点评 本题考查独立性检验知识,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.已知三角形△ABC中,角A,B,C的对边分别为a,b,c,若a=5,b=8,C=60°,则$\overrightarrow{BC}•\overrightarrow{AC}$=( )
| A. | $-20\sqrt{3}$ | B. | -20 | C. | 20 | D. | $20\sqrt{3}$ |
11.直线y=kx+1与圆x2+y2=2的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 均有可能 |
8.某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数).从A类工人中的抽查结果和从B类工人中的抽查结果分别如表1和表2.
表1
表2
(1)先确定x,y,再完成下列频率分布直方图.
(2)估计A类工人生产能力的平均数.(同一组中的数据用该组区间的中点值作代表)
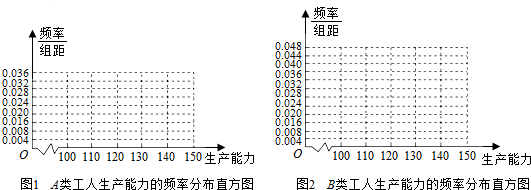
表1
| 生产能力分组 | 人数 |
| [100,110) | 4 |
| [110,120) | 8 |
| [120,130) | x |
| [130,140) | 5 |
| [140,150) | 3 |
| 生产能力分组 | 人数 |
| [110,120) | 6 |
| [120,130) | y |
| [130,140) | 36 |
| [140,150) | 18 |
(2)估计A类工人生产能力的平均数.(同一组中的数据用该组区间的中点值作代表)

15.某人练习射击,共有5发子弹,每次击中目标的概率为0.6,若他只需要在五次射击中四次击中目标就算合格,一旦合格即停止练习.则他在第五次射击结束时恰好合格的概率为( )
| A. | 0.64×0.4 | B. | C${\;}_{5}^{4}$•0.64•(1-0.6)+C${\;}_{5}^{5}$•0.65 | ||
| C. | 0.64 | D. | C${\;}_{4}^{3}$×0.64×0.4 |
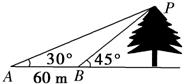 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.