��Ŀ����
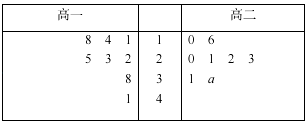
����Ŀ��������������{an}����T={x|x=aj��ai �� i��j}��������{an}���㣺������t��T��ʹ��ֻҪam��ak=t��m��k��N*��m��k��������am+1��ak+1=t�����������{an}��������P��t���� ����������{an}���� ![]() �ж�����{an}�Ƿ��������P��2�����Ƿ��������P��4����
�ж�����{an}�Ƿ��������P��2�����Ƿ��������P��4����
������֤����T���������ǡ�����{an}��������P��0�����ı�Ҫ�����������
������֪{an}�Ǹ���Ϊ�����������У���{an}�Ⱦ�������P��2�����־�������P��5������֤����������N��ʹ��aN �� aN+1 �� aN+2 �� ����aN+k �� ���ǵȲ����У�
���𰸡��⣺���� ![]() ��a2��a1=2����a3��a2=��1��2������{an}����������P��2����
��a2��a1=2����a3��a2=��1��2������{an}����������P��2����
ͬ���ɵã�����{an}��������P��4����
����������ԣ�������������1��1��2��2��1��1��2��2������T={��1��0��1}����������������a2��a1=0��a3��a2=1��
���Բ���������P��0����
����Ҫ�ԣ���Ϊ����{an}��������P��0����
����һ������һ����С����m��k������am��ak=0����am=ak
������P��0���ĺ���ɵ�am+1=ak+1��am+2=ak+2������a2m��k��1=am��1��a2m��k=am����
��������{an}�У��ӵ�k�ʼ�ĸ�����������Թ��ɣ�ak��ak+1������am��1Ϊһ�������еĸ��
��������{an}�������m��1����ͬ���
����T����� ![]() ��Ԫ�أ���T��������
��Ԫ�أ���T��������
����������{an}��������P��2��������{an}��������P��5����
���Դ���M�䡢N�䣬ʹ��aM'+p��aM'=2��aN'+q��aN'=5������p��q�ֱ�������������ϵʽ����С����������
������P��2����P��5���ĺ���ɵã�aM'+p+k��aM'+k=2��aN'+q+k��aN'+k=5��
��M'��N'����ȡk=N'��M'���ɵ�aN'+p��aN'=2��
��M'��N'����ȡk=M'��N'���ɵ�aM'+q��aM'=5��
��M=max{M'��N'}�������aM����aM+p��aM=2��aM+q��aM=5����Ȼp��q��
������P��2����P��5���ĺ���ɵã�aM+p+k��aM+k=2��aN+q+k��aN+k=5��
����aM+qp��aM=��aM+qp��aM+��q��1��p��+��aM+��q��1��p��aM+��q��2��p��+��+��aM+p��aM��=2qaM+qp��aM=��aM+pq��aM+��p��1��q��+��aM+��p��1��q��aM+��p��2��q��+��+��aM+q��aM��=5p
����aM+qp=aM+2q=aM+5p��
����2q=5p��
��p��q������aM+p��aM=2��aM+q��aM=5��������������
����q=5��p=2��aM+2��aM=2��aM+5��aM=5��
���ԣ�aM+2+k��aM+k=2��aM+5+k��aM+k=5��
���ԣ�aM+2k=aM+2��k��1��+2=��=aM+2k��aM+5k=aM+5��k��1��+5=��=aM+5k��
ȡN=M+5����
���ԣ���k��ż������aN+k=aN+k��
��k����������aN+k=aN+5+��k��5��=aN+5+��k��5��=aN+5+��k��5��=aN+k��
���ԣ�aN+k=aN+k
����aN��aN+1��aN+2������aN+k�����ǹ���Ϊ1�ĵȲ�����
�������������� ![]() �ɵ�a2��a1=2����a3��a2=��1��2������{an}����������P��2����ͬ�����ж�����{an}��������P��4��������������������1��1��2��2��1��1��2��2������T={��1��0��1}�������������¶����֤����{an}����������P��0������������Գ�������֤�����Ҫ�Լ��ɣ����������⣬����{an}�Ǹ���Ϊ�����������У���{an}�Ⱦ�������P��2�����־�������P��5������֤�ô�������N��ʹ��aN��aN+1��aN+2������aN+k�����ǵȲ����У�
�ɵ�a2��a1=2����a3��a2=��1��2������{an}����������P��2����ͬ�����ж�����{an}��������P��4��������������������1��1��2��2��1��1��2��2������T={��1��0��1}�������������¶����֤����{an}����������P��0������������Գ�������֤�����Ҫ�Լ��ɣ����������⣬����{an}�Ǹ���Ϊ�����������У���{an}�Ⱦ�������P��2�����־�������P��5������֤�ô�������N��ʹ��aN��aN+1��aN+2������aN+k�����ǵȲ����У�
�����㾫����ͨ������������е�ͨ�ʽ�������������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ�����Խ����⣮

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij��ѧΪ����ѧ����A��B���Ҳ����ò͵�����ȣ�����A��B���Ҳ������ù��͵�ѧ���������ȡ��100�ˣ�ÿ�˷ֱ�������Ҳ����������֣����־�Ϊ60�֣������������ݣ���������10Ϊ���ֳ�6�飺[0��10����[10��20����[20��30����[30��40����[40��50����[50��60]���õ�A����������Ƶ�ʷֲ�ֱ��ͼ����B����������Ƶ���ֲ�����
B��������Ƶ���ֲ��� | |
�������� | Ƶ�� |
[0��10�� | 2 |
[10��20�� | 3 |
[20��30�� | 5 |
[30��40�� | 15 |
[40��50�� | 40 |
[50��60] | 35 |

�����ڳ�����100���У����A�������ֵ���30��������
���Ӷ�B����������[0��20����Χ�ڵ��������ѡ��2�ˣ���2����ǡ��1��������[0��10����Χ�ڵĸ��ʣ�
���������A��B���Ҳ�����ѡ��һ���òͣ����ѡ����һ�ң�˵�����ɣ�