题目内容
【题目】已知椭圆G: ![]() 的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
②存在b使得椭圆G上满足条件的点P仅有两个;
③|OP|的最小值为2,
其中,所有正确命题的序号是 .
【答案】①③
【解析】解:椭圆G: ![]() 的两个焦点分别为
的两个焦点分别为
F1( ![]() ,0)和F2(﹣
,0)和F2(﹣ ![]() ,0),
,0),
短轴的两个端点分别为B1(0,﹣b)和B2(0,b),
设P(x,y),点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|,
由椭圆定义可得,|PB1|+|PB2|=2a=2 ![]() >2b,
>2b,
即有P在椭圆 ![]() +
+ ![]() =1上.
=1上.
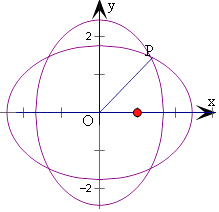
对于①,将x换为﹣x方程不变,则点P的轨迹关于y轴对称,
故①正确;
对于②,由图象可得轨迹关于x,y轴对称,且0<b< ![]() ,
,
则椭圆G上满足条件的点P有4个,
不存在b使得椭圆G上满足条件的点P仅有两个,故②不正确;
对于③,由图象可得,当P满足x2=y2,即有6﹣b2=b2,即b= ![]() 时,
时,
|OP|取得最小值,可得x2=y2=2,即有|OP|的最小值为2,故③正确.
所以答案是:①③.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目