题目内容
【题目】已知函数![]() ,
, ![]() R.
R.
(1)证明:当![]() 时,函数
时,函数![]() 是减函数;
是减函数;
(2)根据![]() 的不同取值,讨论函数
的不同取值,讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)当![]() ,且
,且![]() 时,证明:对任意
时,证明:对任意![]() ,存在唯一的
,存在唯一的![]() R,使得
R,使得![]() ,且
,且![]() .
.
【答案】(1)见解析(2) 当![]() 时,函数
时,函数![]() 是奇函数;当
是奇函数;当![]() 时,函数
时,函数![]() 是偶函数;当
是偶函数;当![]() 且
且![]() 时,函数
时,函数![]() 是非奇非偶函数,(3)见解析
是非奇非偶函数,(3)见解析
【解析】试题分析:
(1)任取![]() ,设
,设![]() ,计算可得
,计算可得 ,据此可得
,据此可得![]() ,函数
,函数![]() 是减函数.
是减函数.
(2)分类讨论可得:当![]() 时,函数
时,函数![]() 是偶函数,当
是偶函数,当![]() 时函数
时函数![]() 是奇函数,当
是奇函数,当![]() 且
且![]() 时,函数
时,函数![]() 是非奇非偶函数.
是非奇非偶函数.
(3)由(1)知,当![]() 时函数
时函数![]() 是减函数,结合函数的单调性分别证明
是减函数,结合函数的单调性分别证明![]() 的存在性(利用函数的值域)和唯一性(利用反证法)即可证得题中的结论.
的存在性(利用函数的值域)和唯一性(利用反证法)即可证得题中的结论.
试题解析:
(1)任取![]() ,设
,设![]() ,则
,则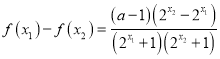 ,
,
∵![]() ,所以
,所以![]() ,又
,又![]() ,∴
,∴![]() ,即
,即![]() ,
,
所以当![]() 时,函数
时,函数![]() 是减函数.
是减函数.
(2)当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 是偶函数,
是偶函数,
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以函数![]() 是奇函数,
是奇函数,
当![]() 且
且![]() 时,
时, ![]() ,
, ![]() ,
,
因为![]() 且
且![]() ,
,
所以函数![]() 是非奇非偶函数.
是非奇非偶函数.
(3)由(1)知,当![]() 时函数
时函数![]() 是减函数,
是减函数,
所以函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
因为![]() ,所以存在
,所以存在![]() ,使得
,使得![]() .
.
假设存在![]() 使得
使得![]() ,
,
若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() ,
,
与![]() 矛盾,故
矛盾,故![]() 是唯一的,
是唯一的,
假设![]() ,即
,即![]() 或
或![]() ,则
,则![]() 或
或![]() ,
,
所以![]() ,与
,与![]() 矛盾,故
矛盾,故![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目