题目内容
在 中,
中,
(1)求角B的大小;
(2)求 的取值范围.
的取值范围.
 中,
中,
(1)求角B的大小;
(2)求
 的取值范围.
的取值范围.(1) 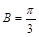 ;(2)
;(2)  .
.
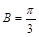 ;(2)
;(2)  .
.试题分析:(1)由正弦定理实现边角互化,再利用两角和与差的正余弦公式化简为
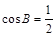 ,再求角
,再求角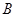 的值;(2)二倍角公式降幂扩角,两角差余弦公式展开,同时注意隐含条件
的值;(2)二倍角公式降幂扩角,两角差余弦公式展开,同时注意隐含条件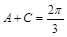 ,即可化为一角一函数
,即可化为一角一函数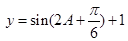 ,再结合
,再结合 求其值域.求解时一定借助函数图象找其最低点与最高点的纵坐标.
求其值域.求解时一定借助函数图象找其最低点与最高点的纵坐标.试题解析:(1)由已知得:
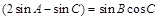 ,
,即
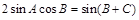
∴
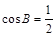
∴
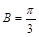 5分
5分(2)由(1)得:
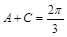 ,故+
,故+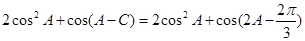
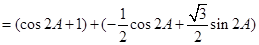
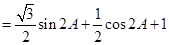
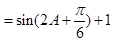
又
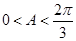 ∴
∴
所以
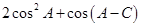 的取值范围是
的取值范围是 . 12分
. 12分
练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
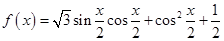 (1)求
(1)求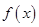 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边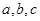 且满足
且满足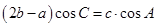 ,求
,求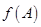 的取值范围.
的取值范围.
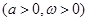 d的最大值为2,
d的最大值为2,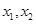 是集合
是集合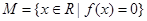 中的任意两个元素,且
中的任意两个元素,且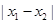 的最小值为
的最小值为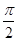 .
.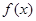 的解析式及其对称轴;
的解析式及其对称轴;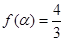 ,求
,求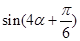 的值.
的值.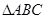 中,
中,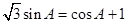 .
. 的大小;
的大小; 的取值范围.
的取值范围. .
. 的最小正周期; (2)求
的最小正周期; (2)求 ,
,
 且函数
且函数 的最小正周期为
的最小正周期为 .
. 的值和函数
的值和函数 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 、
、 、
、 ,又
,又 ,
, ,
, ,求边长
,求边长 .
. 的值;
的值; 的最小正周期及单调递减区间.
的最小正周期及单调递减区间. (x-6)](x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为_____℃.
(x-6)](x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为_____℃.