题目内容
在⊿ABC中,角A,B,C的对边分别为A,b,C,且满足(2A-C)CosB=bCosC.
(Ⅰ)求角B的大小;
(Ⅱ)已知函数f(A,C)=Cos2A+sin2C,求f(A,C)的最大值。
(Ⅰ)求角B的大小;
(Ⅱ)已知函数f(A,C)=Cos2A+sin2C,求f(A,C)的最大值。
(Ⅰ)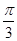 ;(Ⅱ)1+
;(Ⅱ)1+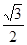 .
.
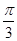 ;(Ⅱ)1+
;(Ⅱ)1+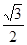 .
.试题分析:(1)利用正弦定理,结合A、B的范围求出求角B的大小;(Ⅱ)把C用A来表示,在
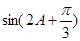 =1时取最大值.
=1时取最大值.试题解析:(Ⅰ)∵ (2A-C)CosB=bCosC ∴ 由正弦定理得
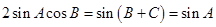
又∵
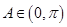 ∴
∴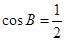
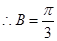
(Ⅱ)
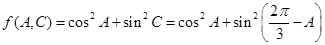
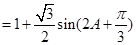
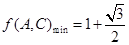

练习册系列答案
相关题目
 (其中
(其中 ),
), 、
、 是函数
是函数 的两个不同的零点,且
的两个不同的零点,且 的最小值为
的最小值为 .
. 的值;
的值; ,求
,求 的值.
的值.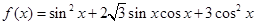 ,
, .求:
.求: 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 上的值域.
上的值域. 中,
中,
 的取值范围.
的取值范围.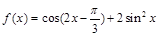 ,
,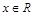 .
.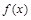 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;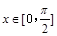 时,求函数
时,求函数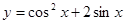 (
(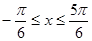 )的值域是_______________。
)的值域是_______________。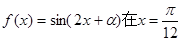 时有极大值,且
时有极大值,且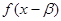 为奇函数,则
为奇函数,则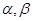 的一组可能值依次为( )
的一组可能值依次为( )



 ,
, .
. 时,求函数
时,求函数 的最大值;
的最大值; 上的任 意一个
上的任 意一个 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围. .
.