题目内容
某开发商用9000万元在市区购买一块土地建一幢写字楼,规划要求写字楼每层建筑面积为2000平方米.已知该写字楼第一层的建筑费用为每平方米4000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.
(1)若该写字楼共x层,总开发费用为y万元,求函数y=f(x)的表达式;(总开发费用=总建筑费用+购地费用)
(2)要使整幢写字楼每平方米的平均开发费用最低,该写字楼应建为多少层?
(1)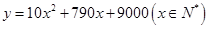 ;(2)30.
;(2)30.
解析试题分析:(1)经审题,先算出第一层楼的建筑费用,由条件“从第二层开始,每一层的建筑费用比其下面一层每平方米增加100元.”可知,各楼层的建筑费用成等差数列,首项为第一层的建筑费用,公差为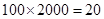 (万元),再根据等差数列前
(万元),再根据等差数列前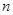 项和公式可得出总开发费用的函数
项和公式可得出总开发费用的函数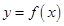 的表达式;(2)由(1)知每平方米的平均开发费用为
的表达式;(2)由(1)知每平方米的平均开发费用为 元,构造函数
元,构造函数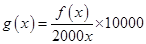 ,并由基本不等式求出函数
,并由基本不等式求出函数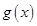 的最小值,注意自变量
的最小值,注意自变量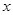 是正整数.
是正整数.
试题解析:(1)由已知,写字楼最下面一层的总建筑费用为: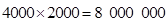 (元)
(元)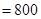 (万元),
(万元),
从第二层开始,每层的建筑总费用比其下面一层多: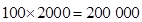 (元)
(元)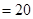 (万元),
(万元),
写字楼从下到上各层的总建筑费用构成以800为首项,20为公差的等差数列,
所以函数表达式为: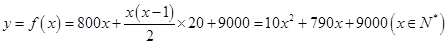 . 6分
. 6分
(2)由(1)知写字楼每平方米平均开发费用为: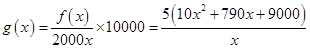
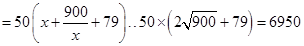 (元). 10分
(元). 10分
当且仅当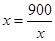 时,即
时,即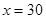 时等号成立.
时等号成立.
答:该写字楼建为30层时,每平方米平均开发费用最低. 12分
考点:1.函数建模;2.基本不等式.

练习册系列答案
相关题目
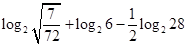 ;
;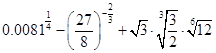 .
. ,其中
,其中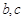 为常数.
为常数.  在区间
在区间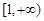 上单调,求
上单调,求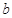 的取值范围;
的取值范围;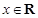 ,都有
,都有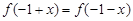 成立,且函数
成立,且函数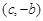 ,
,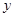 (单位:千套)与销售价格
(单位:千套)与销售价格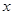 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式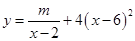 ,其中
,其中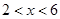 ,
,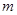 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.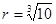 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.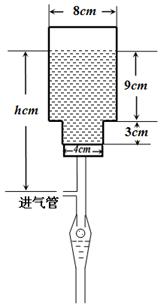
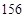 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?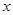 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为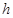 (单位:厘米),已知当
(单位:厘米),已知当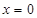 时,
时,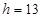 .试将
.试将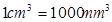 )
) ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式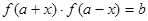 对定义域中的每一个
对定义域中的每一个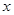 都成立,则称函数
都成立,则称函数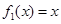 是否为 “(
是否为 “(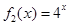 是“(
是“(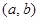 ;,
;, 是“(
是“(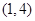 .当
.当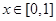 时,
时,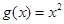
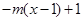
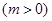 ,若当
,若当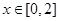 时,都有
时,都有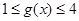 ,试求
,试求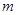 的取值范围.
的取值范围.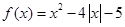 .
.
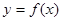 的图象;
的图象;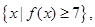 求集合A;
求集合A;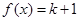 有两解,求实数
有两解,求实数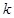 的取值范围.
的取值范围.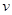 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当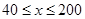 时,车流速度
时,车流速度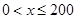 时,求函数
时,求函数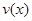 的表达式;
的表达式;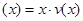 ,
,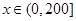 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.