题目内容
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度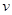 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当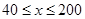 时,车流速度
时,车流速度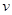 是车流密度
是车流密度 的一次函数.(1)当
的一次函数.(1)当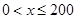 时,求函数
时,求函数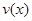 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位: 辆/小时)f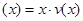 ,
,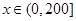 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.
(1)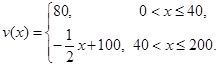 (2)即当车流密度为100辆/千米时,车流量可以达到最大,最大值为5000辆/小时.
(2)即当车流密度为100辆/千米时,车流量可以达到最大,最大值为5000辆/小时.
解析试题分析:(1)本题是一个分段函数,当车流量小于等于40时,速度为80千米/小时,当车流量大于40时小于或等于200时通过两端点解出一次函数的解析式.(2)通过计算分段函数一个是一次函数,一个是二次函数来确定最大值.本题属于分段函数的应用,这类应用题关键就是审清题意.分段函数的最大值是分别求出各段函数的最大值,在求出总的最大值,这种思维要有.
试题解析:解:(1)由题意:当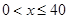 时,
时,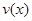 =80;当
=80;当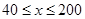 时,设
时,设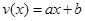 ,
,
再由已知得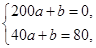 解得
解得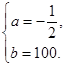
故函数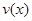 的表达式为
的表达式为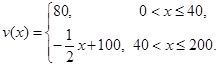 5分
5分
(2)依题意并由(1)可得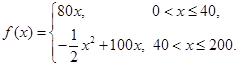
当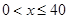 时,
时,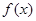 为增函数,故当
为增函数,故当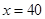 时,其最大值为
时,其最大值为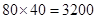 ;
;
当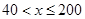 时,
时,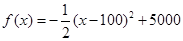 ;
;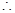 当
当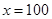 时,
时,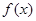 有最大值5000.
有最大值5000.
综上,当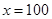 时,
时,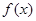 在区间
在区间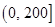 上取得最大值5000.
上取得最大值5000.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值为5000辆/小时. 10分
考点:

某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费
元计费
(Ⅰ)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(Ⅱ)已知小王家第一季度缴费情况如下:
| 月份 | 1 | 2 | 3 | 合计 |
| 缴费金额 | 87元 | 62元 | 45元8角 | 194元8角 |
某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
若每月用气量不超过最低额度
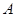
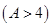 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费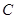
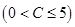 元;若用气量超过
元;若用气量超过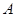 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付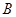 元.
元.⑴根据上面的表格求
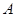 、
、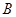 、
、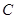 的值;
的值;⑵若用户第四月份用气30立方米,则应交煤气费多少元?
 是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛
是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛 ,要求:B在
,要求:B在 上,D在
上,D在 上,对角线
上,对角线 过C点, 且矩形
过C点, 且矩形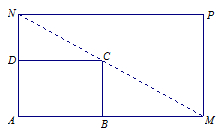
 米,矩形
米,矩形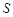 平方米,试用解析式将
平方米,试用解析式将 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).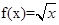 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。 有最小值为-12,求实数
有最小值为-12,求实数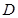 上的函数
上的函数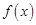 ,如果满足:对任意
,如果满足:对任意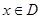 ,存在常数
,存在常数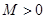 ,使得
,使得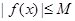 成立,则称
成立,则称 是
是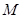 称为函数
称为函数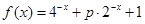 ,
,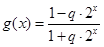 .
.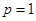 时,求函数
时,求函数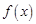 在
在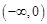 上的值域,并判断函数
上的值域,并判断函数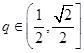 ,函数
,函数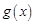 在
在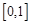 上的上界是
上的上界是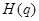 ,求
,求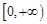 上是以
上是以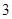 为上界的有界函数, 求实数
为上界的有界函数, 求实数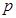 的取值范围.
的取值范围.