题目内容
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式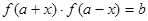 对定义域中的每一个
对定义域中的每一个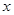 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(Ⅰ)判断函数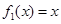 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(Ⅱ)若函数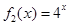 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对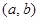 ;,
;,
(Ⅲ)已知函数 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对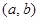 为
为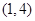 .当
.当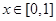 时,
时,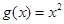
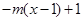
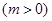 ,若当
,若当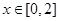 时,都有
时,都有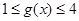 ,试求
,试求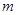 的取值范围.
的取值范围.
(Ⅰ)详见解析;(Ⅱ)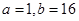 (答案还有其他可能);(Ⅲ)
(答案还有其他可能);(Ⅲ)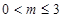
解析试题分析:(Ⅰ) 由给出的定义可知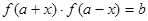 展开后的方程中如果不含x说明对任意x都成立,则函数
展开后的方程中如果不含x说明对任意x都成立,则函数 是“(
是“( )型函数” ,如果展开后的方程含x,则根据方程只能求出某个或某些x满足要求而不是每一个x都符合,则函数
)型函数” ,如果展开后的方程含x,则根据方程只能求出某个或某些x满足要求而不是每一个x都符合,则函数 不是“(
不是“( )型函数(Ⅱ)根据定义列出方程 ,满足方程的实数对应有无数对,只取其中一对就可以(Ⅲ)难度系数较大,应先根据题意分析出当
)型函数(Ⅱ)根据定义列出方程 ,满足方程的实数对应有无数对,只取其中一对就可以(Ⅲ)难度系数较大,应先根据题意分析出当 时,
时, 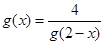 ,此时
,此时 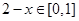 。根据已知
。根据已知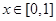 时,
时,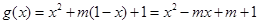 ,其对称轴方程为
,其对称轴方程为 。属动轴定区间问题需分类讨论,在每类中得出
。属动轴定区间问题需分类讨论,在每类中得出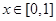 时
时 的值域即
的值域即 的值域,从而得出
的值域,从而得出 时
时 的值域,把两个值域取并集即为
的值域,把两个值域取并集即为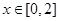 的
的 的值域,由
的值域,由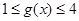 可知
可知 的值域是
的值域是 的子集,列出关于m的不等式即可求解。
的子集,列出关于m的不等式即可求解。
试题解析:(1)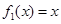 不是“(
不是“( )型函数”,因为不存在实数对
)型函数”,因为不存在实数对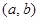 使得
使得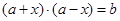 ,
,
即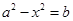 对定义域中的每一个
对定义域中的每一个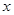 都成立;
都成立;
(2)由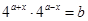 ,得
,得 ,所以存在实数对,
,所以存在实数对,
如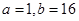 ,使得
,使得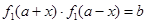 对任意的
对任意的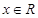 都成立;
都成立;
(3)由题意得, ,所以当
,所以当 时,
时, 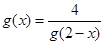 ,其中
,其中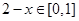 ,而
,而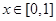 时,
时,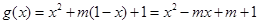 ,其对称轴方程为
,其对称轴方程为 .
.
当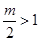 ,即
,即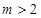 时,
时, 在
在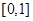 上的值域为
上的值域为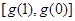 ,即
,即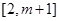 ,则
,则 在
在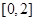 上的值域为
上的值域为 ,由题意得
,由题意得 ,从而
,从而 ;
;
当 ,即
,即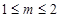 时,
时, 的值域为
的值域为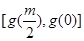 ,即
,即 ,则
,则 在
在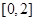 上的值域为
上的值域为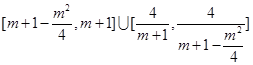 ,则由题意,得
,则由题意,得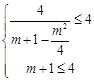 且
且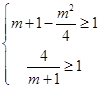 ,解得
,解得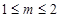 ;
;
当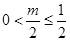 ,即
,即 时,
时, 的值域为
的值域为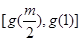 ,即
,即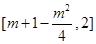 ,则
,则 在
在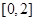 上的值域为
上的值域为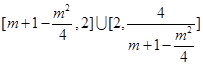 ,即
,即 ,则
,则 ,解得
,解得 .
.
综上所述,所求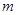 的取值范围是
的取值范围是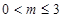

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 两城相距
两城相距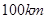 ,在两地之间距
,在两地之间距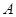 城
城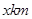 处
处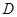 地建一核电站给
地建一核电站给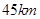 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(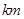 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数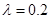 ,若
,若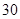 亿度/月,
亿度/月,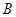 城为
城为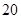 亿度/月.
亿度/月. 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;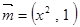 ,
,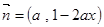 ,其中
,其中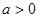 .函数
.函数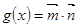 在区间
在区间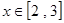 上有最大值为4,设
上有最大值为4,设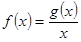 .
.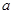 的值;
的值; 在
在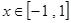 上恒成立,求实数
上恒成立,求实数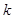 的取值范围.
的取值范围. 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
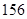 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?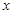 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,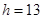 .试将
.试将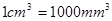 )
) ,点
,点 、
、 在函数
在函数 的图象上,
的图象上, 在函数
在函数 的图象上,设
的图象上,设
 .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前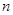 项和为
项和为 ;
; ,记数列
,记数列 的前
的前 ,数列
,数列 的前
的前 ,试比较
,试比较 的大小.
的大小. 千件,需另投入成本为
千件,需另投入成本为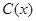 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量 是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛
是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛 ,要求:B在
,要求:B在 上,D在
上,D在 上,对角线
上,对角线 过C点, 且矩形
过C点, 且矩形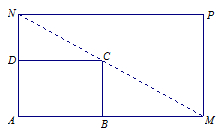
 米,矩形
米,矩形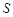 平方米,试用解析式将
平方米,试用解析式将
 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数 的取值范围。
的取值范围。 有最小值为-12,求实数
有最小值为-12,求实数