题目内容
已知函数 ,其中
,其中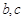 为常数.
为常数.
(Ⅰ)若函数 在区间
在区间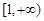 上单调,求
上单调,求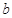 的取值范围;
的取值范围;
(Ⅱ)若对任意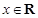 ,都有
,都有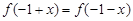 成立,且函数
成立,且函数 的图象经过点
的图象经过点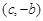 ,
,
求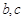 的值.
的值.
(I)  ;(Ⅱ)c=-1或c=-2.
;(Ⅱ)c=-1或c=-2.
解析试题分析:(I)一元二次函数开口向上时,在对称轴的左侧单减,在对称轴的右侧单增,对称轴公式为x=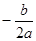 ,由题,
,由题,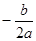 ≤1,解得
≤1,解得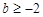 ;(Ⅱ)若
;(Ⅱ)若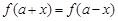 ,则f(x)关于x=a对称,由题,x=-1,所以b=2,将点(c,-b)代入解析式,有 c=-1或c=-2.
,则f(x)关于x=a对称,由题,x=-1,所以b=2,将点(c,-b)代入解析式,有 c=-1或c=-2.
试题解析:(I)∵函数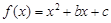 ,
,
∴它的开口向上,对称轴方程为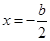 ,
,
∵函数 在区间
在区间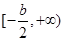 上单调递增,
上单调递增,
∴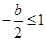 ,
,
∴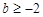 .
.
(Ⅱ)∵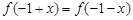 ,
,
∴函数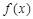 的对称轴方程为
的对称轴方程为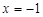 ,
,
∴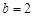 .
.
又∵函数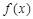 的图象经过点
的图象经过点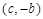 ,
,
∴有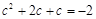 ,
,
即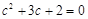 ,
,
∴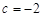 或
或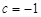 .
.
考点:一元二次函数的和对称性.

练习册系列答案
相关题目
 (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和. 两城相距
两城相距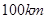 ,在两地之间距
,在两地之间距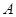 城
城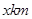 处
处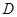 地建一核电站给
地建一核电站给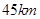 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离(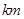 )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数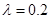 ,若
,若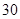 亿度/月,
亿度/月,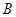 城为
城为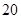 亿度/月.
亿度/月. 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;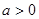 且
且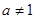 ,函数
,函数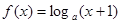 ,
,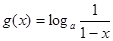 ,记
,记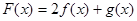
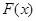 的定义域及其零点;
的定义域及其零点; 的方程
的方程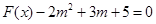 在区间
在区间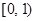 内仅有一解,求实数
内仅有一解,求实数 的取值范围.
的取值范围. .
. 有两个零点,求
有两个零点,求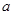 的取值范围;
的取值范围; 与
与 上各有一个零点,求
上各有一个零点,求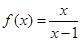 .
.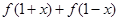 的值;
的值; 在
在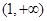 上是减函数.
上是减函数.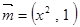 ,
,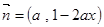 ,其中
,其中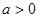 .函数
.函数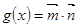 在区间
在区间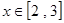 上有最大值为4,设
上有最大值为4,设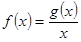 .
.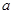 的值;
的值; 在
在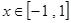 上恒成立,求实数
上恒成立,求实数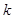 的取值范围.
的取值范围. 是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛
是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛 ,要求:B在
,要求:B在 上,D在
上,D在 上,对角线
上,对角线 过C点, 且矩形
过C点, 且矩形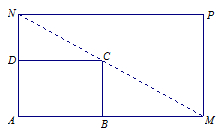
 米,矩形
米,矩形 平方米,试用解析式将
平方米,试用解析式将