题目内容
两条曲线的方程分别是f1（x，y）=0和f2（x，y）=0，它们的交点是P（x0，y0），若曲线C的方程为λ1f1（x，y）+λ2f2（x，y）=0 （λ1、λ2不全为0），则有（ ）
| A、曲线C恒经过点P |
| B、仅当λ1=0，λ2≠0时曲线C经过点P |
| C、仅当λ2=0，λ1≠0时曲线C经过点P |
| D、曲线C不经过点P |
考点：曲线与方程
专题：计算题,直线与圆
分析：根据曲线和方程之间的关系进行判断．
解答：
解：∵P（x0，y0），是f1（x，y）=0，f2（x，y）=0的交点，∴f1（x0，y0）=0，f2（x0，y0）=0，
则方程λ1f1（x0，y0）+λ2f2（x0，y0）=0，即方程λ1f1（x0，y0）+λ2f2（x0，y0）=0，
故选：A．
则方程λ1f1（x0，y0）+λ2f2（x0，y0）=0，即方程λ1f1（x0，y0）+λ2f2（x0，y0）=0，
故选：A．
点评：本题考查曲线和方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
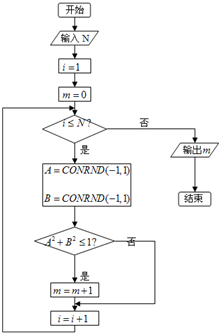如图的程序框图可用来估计π的值（假设函数CONRND（-1，1）是产生随机数的函数，它能随机产生区间（-1，1）内的任何一个实数）．如果输入1000，输出的结果为788，则由此可估计π的近似值为（ ）| A、3.141 |
| B、3.142 |
| C、3.151 |
| D、3.152 |
已知0＜a＜b，且a+b=1，下列不等式中，一定成立的是（ ）
①log2a＞-1；②log2a+log2b＞-2；③log2（b-a）＜0；④log2（
+
）＞1．
①log2a＞-1；②log2a+log2b＞-2；③log2（b-a）＜0；④log2（
| b |
| a |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、①④ |
已知直线2ax-by+2=0（a＞0，b＞0）平分圆C：x2+y2+2x-4y+1=0的圆周长，则
+
的最小值为（ ）
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
| C、4 | ||
| D、6 |