题目内容
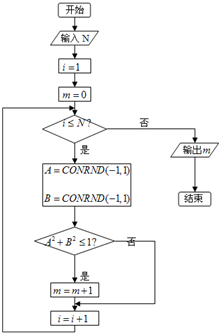 如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )
如图的程序框图可用来估计π的值(假设函数CONRND(-1,1)是产生随机数的函数,它能随机产生区间(-1,1)内的任何一个实数).如果输入1000,输出的结果为788,则由此可估计π的近似值为( )| A、3.141 |
| B、3.142 |
| C、3.151 |
| D、3.152 |
考点:程序框图
专题:计算题,算法和程序框图
分析:根据已知中CONRND(-1,1)是产生均匀随机数的函数,它能随机产生区间(-1,1)内的任何一个实数,及已知中的程序框图,我们可分析出程序的功能是利用随机模拟实验的方法求任取(-1,1)上的两个数A,B,求A2+B2≤1的概率,分别计算出满足A∈(-1,1),B∈(-1,1)和A2+B2≤1对应的平面区域的面积,代入几何概型公式,即可得到答案
解答:
解:根据已知中的流程图我们可以得到
该程序的功能是利用随机模拟实验的方法求任取(-1,1)上的两个数A,B,求A2+B2≤1的概率
∵A∈(-1,1),B∈(-1,1),对应的平面区域面积为:2×2=4
而A2+B2≤1对应的平面区域的面积为:π
故m=
=
,⇒π=3.152
故选:D.
该程序的功能是利用随机模拟实验的方法求任取(-1,1)上的两个数A,B,求A2+B2≤1的概率
∵A∈(-1,1),B∈(-1,1),对应的平面区域面积为:2×2=4
而A2+B2≤1对应的平面区域的面积为:π
故m=
| π |
| 4 |
| 788 |
| 1000 |
故选:D.
点评:本题考查的知识点是程序框图,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键,本题属于基本知识的考查.

练习册系列答案
相关题目
满足{a,b}∪B={a,b,c}的集合B的个数是( )
| A、1 | B、2 | C、3 | D、4 |
若实数x,y满足不等式
,且目标函数z=x-2y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
两条曲线的方程分别是f1(x,y)=0和f2(x,y)=0,它们的交点是P(x0,y0),若曲线C的方程为λ1f1(x,y)+λ2f2(x,y)=0 (λ1、λ2不全为0),则有( )
| A、曲线C恒经过点P |
| B、仅当λ1=0,λ2≠0时曲线C经过点P |
| C、仅当λ2=0,λ1≠0时曲线C经过点P |
| D、曲线C不经过点P |
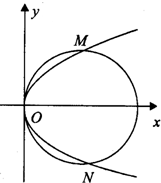 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且