题目内容
已知直线2ax-by+2=0(a>0,b>0)平分圆C:x2+y2+2x-4y+1=0的圆周长,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
| C、4 | ||
| D、6 |
考点:基本不等式在最值问题中的应用,直线与圆的位置关系
专题:不等式的解法及应用,直线与圆
分析:利用直线2ax-by+2=0(a>0,b>0)始终平分圆x2+y2+2x-4y+1=0的圆周,可得圆的圆心(-1,2)在直线2ax-by+2=0(a>0,b>0)上,再利用“1”的代换,结合基本不等式,即可求出
+
的最小值.
| 1 |
| a |
| 2 |
| b |
解答:
解:由题意,圆的圆心(-1,2)在直线2ax-by+2=0(a>0,b>0)上
∴-2a-2b+2=0(a>0,b>0)
∴a+b=1
∴
+
=(a+b)(
+
)=3+
+
≥3+2
=3+2
,当且仅当
=
,即a=
-1,b=2-
时,
+
的最小值为3+2
.
故选:B.
∴-2a-2b+2=0(a>0,b>0)
∴a+b=1
∴
| 1 |
| a |
| 2 |
| b |
| 1 |
| a |
| 2 |
| b |
| b |
| a |
| 2a |
| b |
|
| 2 |
| b |
| a |
| 2a |
| b |
| 2 |
| 2 |
| 1 |
| a |
| 2 |
| b |
| 2 |
故选:B.
点评:本题考查圆的对称性,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
两条曲线的方程分别是f1(x,y)=0和f2(x,y)=0,它们的交点是P(x0,y0),若曲线C的方程为λ1f1(x,y)+λ2f2(x,y)=0 (λ1、λ2不全为0),则有( )
| A、曲线C恒经过点P |
| B、仅当λ1=0,λ2≠0时曲线C经过点P |
| C、仅当λ2=0,λ1≠0时曲线C经过点P |
| D、曲线C不经过点P |
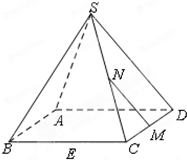 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC1;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( )
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC1;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( )