题目内容
已知函数f(x)=ax2+(2a+1)x+1-3a,其中(a≠0)
(1)若函数在(-∞,2]上单调递增,求a的范围;
(2)若f(lgx)=0的两根之积为10,求a的值;
(3)若g(x)=
,是否存在实数a,使得g(g(x))=0只有一个实数根?若存在,求出a的值或者范围,若不存在,说明理由.
(1)若函数在(-∞,2]上单调递增,求a的范围;
(2)若f(lgx)=0的两根之积为10,求a的值;
(3)若g(x)=
| f(x) |
| a |
考点:二次函数的性质,对数的运算性质
专题:函数的性质及应用
分析:(1)根据二次函数的单调性即可求得a的范围;
(2)设lgx=t,则得到方程at2+(2a+1)t+1-3a=0,则t1+t2=-
=lg(x1x2)=1,x1,x2是原方程的两实根,这样解出a即可;
(3)先求g(x)=x2+
x+
,求得△=
+16>0,所以方程g(x)=0有两不等实根.而由g(g(x))=0得,g2(x)+
g(x)+
=0,所以可令g(x)=t,所以t2+
t+
=0,而该方程有两不等实根,并设为t1,t2,所以有g(x)=t1,或g(x)=t2,根据题意便知这两个方程只有一个解,并且可设g(x)=t1无解,g(x)=t2有一个解,根据判别式的取值情况即可得到
,而根据韦达定理即可得到关于a的不等式,解不等式即得a的取值.
(2)设lgx=t,则得到方程at2+(2a+1)t+1-3a=0,则t1+t2=-
| 2a+1 |
| a |
(3)先求g(x)=x2+
| 2a+1 |
| a |
| 1-3a |
| a |
| 1 |
| a2 |
| 2a+1 |
| a |
| 1-3a |
| a |
| 2a+1 |
| a |
| 1-3a |
| a |
|
解答:
解:(1)f(x)为二次函数,对称轴为x=
;
∴若函数在(-∞,2]上单调递增,则:
,解得,-
≤a<0;
∴a的范围为[-
,0);
(2)设f(lgx)=0的两根为x1,x2,令t=lgx,则:
t1=lgx1,t2=lgx2为方程at2+(2a+1)t+1-3a=0的两根;
则:∴t1+t2=lgx1+lgx2=lgx1x2=lg10=1;
即:t1+t2=
=1,∴a=-
;
经检验a=-
时,原方程有两个根,所以a的值为-
;
(3)g(x)=
=x2+
x+
,令
=p,
=q;
因为△=p2-4q=
+16>0恒成立,则方程x2+px+q=0有两不等实根;
由g(g(x))=0得,g2(x)+pg(x)+q=0,令g(x)=t,则得到:
t2+pt+q=0,该方程有两不等实根,设为t1,t2,则:
g(x)=t1,或g(x)=t2,(t1≠t2);
即x2+px+q=t1,或x2+px+q=t2,根据题意,这两个方程只有一个解;
不妨设x2+px+q=t1无解,x2+px+q=t2只有一个解;
∴
;
∴
;
又q-
=
-
=
-3-1-
-
<-4;
∴
;
即方程t2+pt+q=0的两根都小于-4;
根据韦达定理得:
,解得:a∈∅;
所以不存在这样的a.
| 2a+1 |
| -2a |
∴若函数在(-∞,2]上单调递增,则:
|
| 1 |
| 6 |
∴a的范围为[-
| 1 |
| 6 |
(2)设f(lgx)=0的两根为x1,x2,令t=lgx,则:
t1=lgx1,t2=lgx2为方程at2+(2a+1)t+1-3a=0的两根;
则:∴t1+t2=lgx1+lgx2=lgx1x2=lg10=1;
即:t1+t2=
| 2a+1 |
| -a |
| 1 |
| 3 |
经检验a=-
| 1 |
| 3 |
| 1 |
| 3 |
(3)g(x)=
| f(x) |
| a |
| 2a+1 |
| a |
| 1-3a |
| a |
| 2a+1 |
| a |
| 1-3a |
| a |
因为△=p2-4q=
| 1 |
| a2 |
由g(g(x))=0得,g2(x)+pg(x)+q=0,令g(x)=t,则得到:
t2+pt+q=0,该方程有两不等实根,设为t1,t2,则:
g(x)=t1,或g(x)=t2,(t1≠t2);
即x2+px+q=t1,或x2+px+q=t2,根据题意,这两个方程只有一个解;
不妨设x2+px+q=t1无解,x2+px+q=t2只有一个解;
∴
|
∴
|
又q-
| p2 |
| 4 |
| 1-3a |
| a |
| (2a+1)2 |
| 4a2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 4a2 |
∴
|
即方程t2+pt+q=0的两根都小于-4;
根据韦达定理得:
|
所以不存在这样的a.
点评:考查二次函数的单调性及单调区间,韦达定理,一元二次方程解的情况和判别式△的关系.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
两条曲线的方程分别是f1(x,y)=0和f2(x,y)=0,它们的交点是P(x0,y0),若曲线C的方程为λ1f1(x,y)+λ2f2(x,y)=0 (λ1、λ2不全为0),则有( )
| A、曲线C恒经过点P |
| B、仅当λ1=0,λ2≠0时曲线C经过点P |
| C、仅当λ2=0,λ1≠0时曲线C经过点P |
| D、曲线C不经过点P |
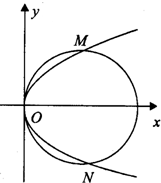 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且