题目内容

若椭圆
x2
100
+
y2
36
=1上一点P到焦点F1的距离为6，那么点P到另一个焦点F2的距离等于
 
．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据椭圆的定义可得|PF1|+|PF2|=2a，根据椭圆
x2
100
+
y2
36
=1上一点P到焦点F1的距离等于6，可求点P到另一个焦点F2的距离
解答： 解：根据椭圆的定义可得|PF1|+|PF2|=2a，
∵椭圆
x2
100
+
y2
36
=1上一点P到焦点F1的距离等于6
∴6+|PF2|=20
∴|PF2|=14
故答案为：14
点评：本题的考点是椭圆的定义，主要考查椭圆定义的运用，属于基础题．
练习册系列答案
相关题目
根据程序框图输出的结果t=
 
．
下列命题中正确命题的个数是（　　）
（1）设p：（x-2）（y-5）≠0；q：x≠2或y≠5，则p是q的充分不必要条件；
（2）一组有六个数的数据是1，2，3，3，4，5的平均数、众数、中位数都相同；
（3）在△ABC中，a=4，b=4
3
，A=30°，则角B等于30°；
（4）对命题p：?x0∈R，使得x02+x0+1＜0，则?p：?x∈R，均有x2+x+1≥0．
A、1B、2C、3D、4
某企业2010年的利润是1200万元，计划从2011年起每年比上一年利润增加200万元，若经过x年累计利润为y万元，试写出y是x的函数关系式．
已知数列{an}的前n项的和为Sn，a1=-
1
2
，an+1=
2an+1，an≤0
an-
3
4
，an＞0
，则S2015=
 
．
两条曲线的方程分别是f1（x，y）=0和f2（x，y）=0，它们的交点是P（x0，y0），若曲线C的方程为λ1f1（x，y）+λ2f2（x，y）=0 （λ1、λ2不全为0），则有（　　）
A、曲线C恒经过点P
B、仅当λ1=0，λ2≠0时曲线C经过点P
C、仅当λ2=0，λ1≠0时曲线C经过点P
D、曲线C不经过点P
已知函数f（x）=
1
x
+3，数列{an}的各项均为正数，a1=1，且a
 
2
n+1
=
1
f(
a
2
n
)
（n∈N*）．
（Ⅰ）证明：数列（
1
a
2
n
）为等差数列；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）数列{bn}满足bn•
(1-n)
a
2
n
+n
a
2
n
=2n，若bn≥m对任意的正整数n恒成立，求m的取值范围．
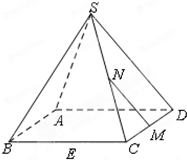如图，在正四棱锥S-ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论：①EP⊥AC1；②EP∥BD；③EP∥面SBD；④EP⊥面SAC．中恒成立的为（　　）
A、①③B、③④C、①②D、②③④
从集合A={1，2，3}和B={1，4，5，6}中各取一个元素作为点的坐标，则在直角坐标系中能确定不同点的个数是
 
 个．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网