题目内容
已知函数f(x)=|x-k|+|x-2k|(k>0),若当3≤x≤4时,f(x)能取到最小值,则实数k的取值范围是 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由绝对值的意义可得当k≤x≤2k时,函数取得最小值为k.而已知当3≤x≤4时,f(x)能取到最小值,故有k≤3<4≤2k,由此求得k的范围.
解答:
解:根据绝对值的意义,函数f(x)=|x-k|+|x-2k|(k>0)表示数轴上的x对应点到k、2k对应点的距离之和,
故当k≤x≤2k时,函数取得最小值为k.
而已知当3≤x≤4时,f(x)能取到最小值,故有[3,4]⊆[k,2k],
∴k≤3,且4≤2k,求得 2≤k≤3,
故答案为:[2,3].
故当k≤x≤2k时,函数取得最小值为k.
而已知当3≤x≤4时,f(x)能取到最小值,故有[3,4]⊆[k,2k],
∴k≤3,且4≤2k,求得 2≤k≤3,
故答案为:[2,3].
点评:本题主要考查绝对值的意义,集合间的包含关系,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
若实数x,y满足不等式
,且目标函数z=x-2y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
两条曲线的方程分别是f1(x,y)=0和f2(x,y)=0,它们的交点是P(x0,y0),若曲线C的方程为λ1f1(x,y)+λ2f2(x,y)=0 (λ1、λ2不全为0),则有( )
| A、曲线C恒经过点P |
| B、仅当λ1=0,λ2≠0时曲线C经过点P |
| C、仅当λ2=0,λ1≠0时曲线C经过点P |
| D、曲线C不经过点P |
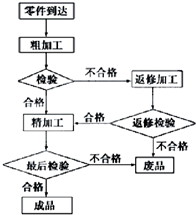 某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了
某工厂加工某种零件有三道工序:粗加工,返修加工和精加工.上面是这个零件加工过程的流程图.已知这个零件最后成了废品,则最多经过了