题目内容
(10分)如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(1)求证:MN//平面PAD
(2)求证:MN⊥CD
(3)若∠PDA=45°,求证:MN⊥平面PCD.
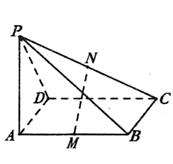
(1)求证:MN//平面PAD
(2)求证:MN⊥CD
(3)若∠PDA=45°,求证:MN⊥平面PCD.

证明:(1)如图,取PD的中点E,连结AE、EN则有EN//CD//AB//AM,
且EN=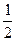 CD=
CD=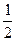 AB=MA.
AB=MA.
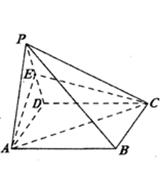
∴四边形AMNE是平行四边形.
∴MN//AE.
∵AE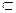 平面PAD,MN
平面PAD,MN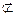 平面PAD,
平面PAD,
∴MN//平面PAD. …………3分
(2)∵PA⊥平面ABCD,∴PA⊥AB.
又AD⊥AB,∴AB⊥平面PAD.
∴AB⊥AE,即AB⊥MN.又CD//AB,
∴MN⊥CD. …………6分
(3)∵PA⊥平面ABCD,∴PA⊥AD.
又∠PAD=45°,E是PD中点,
∴AE⊥PD,即MN⊥PD.
又MN⊥CD,∴MN⊥平面PCD.…………10分
且EN=
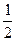 CD=
CD=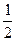 AB=MA.
AB=MA.
∴四边形AMNE是平行四边形.
∴MN//AE.
∵AE
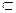 平面PAD,MN
平面PAD,MN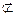 平面PAD,
平面PAD,∴MN//平面PAD. …………3分
(2)∵PA⊥平面ABCD,∴PA⊥AB.
又AD⊥AB,∴AB⊥平面PAD.
∴AB⊥AE,即AB⊥MN.又CD//AB,
∴MN⊥CD. …………6分
(3)∵PA⊥平面ABCD,∴PA⊥AD.
又∠PAD=45°,E是PD中点,
∴AE⊥PD,即MN⊥PD.
又MN⊥CD,∴MN⊥平面PCD.…………10分
略

练习册系列答案
相关题目
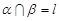 ,
,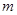 是
是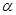 内不同于
内不同于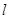 的直线,那么下列命题中错误的是( )
的直线,那么下列命题中错误的是( ) 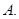 若
若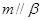 ,则
,则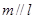
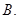 若
若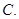 若
若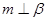 ,则
,则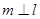
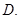 若
若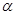 、
、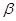 、
、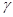 和直线
和直线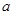 、
、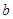 、m、n,下列命题中真命题是( )
、m、n,下列命题中真命题是( ) ,则
,则
 ,则
,则
 ,则
,则
 则
则
 中,
中, ,正方形
,正方形 所在的平面和平面
所在的平面和平面 是
是 的中点,
的中点, 是
是 的交点.
的交点.
 平面
平面 ;
; 平面
平面
 ‖直线
‖直线 ,且
,且 ,则
,则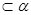
 )第一题满分5分,第二题满分5分,第三题满分8分.
)第一题满分5分,第二题满分5分,第三题满分8分. 条交线ED,CB, E1 D1的关系。
条交线ED,CB, E1 D1的关系。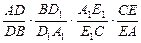 的值;
的值;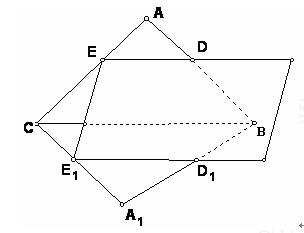
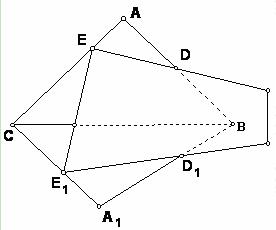
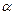 ,
,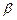 是两个不同的平面,下面四个命题:①若
是两个不同的平面,下面四个命题:①若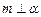 ,
,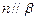 ,
,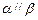 ,则
,则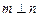 ;②若
;②若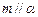 ,则
,则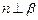 ;④若
;④若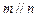 ,
,