题目内容
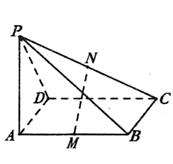
如图,平行四边形 中,
中, ,正方形
,正方形 所在的平面和平面
所在的平面和平面 垂直,
垂直, 是
是 的中点,
的中点, 是
是 的交点.
的交点.

(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面 .
.
 中,
中, ,正方形
,正方形 所在的平面和平面
所在的平面和平面 垂直,
垂直, 是
是 的中点,
的中点, 是
是 的交点.
的交点.
(1)求证:
 平面
平面 ;
;(2)求证:
 平面
平面 .
.证明:⑴ 是
是 的交点,∴
的交点,∴ 是
是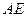 中点,又
中点,又 是
是 的中点,∴
的中点,∴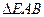 中,
中,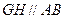 ,
, 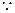
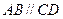 ,∴
,∴
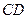 ,又∵
,又∵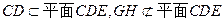
∴ 平面
平面
⑵平面
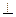 平面
平面 ,交线为
,交线为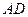 ,∵
,∵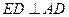 ,
,
∴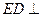 平面
平面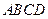 ,∴
,∴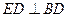 ,又∵
,又∵ ,
,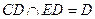
∴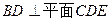
 是
是 的交点,∴
的交点,∴ 是
是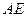 中点,又
中点,又 是
是 的中点,∴
的中点,∴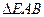 中,
中,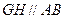 ,
, 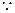
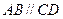 ,∴
,∴
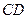 ,又∵
,又∵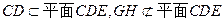
∴
 平面
平面
⑵平面

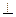 平面
平面 ,交线为
,交线为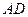 ,∵
,∵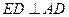 ,
,
∴
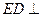 平面
平面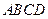 ,∴
,∴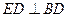 ,又∵
,又∵ ,
,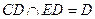
∴
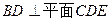
略

练习册系列答案
相关题目





 ;
; 上是否存在点
上是否存在点 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 

 使
使 若存在,求出
若存在,求出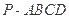 中,
中,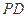 ⊥底面
⊥底面
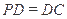 ,
, ,
,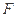 分别是
分别是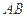
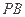 的中点.
的中点.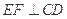 ;(2)设PD="AD=a," 求三棱锥B-EFC的体积.
;(2)设PD="AD=a," 求三棱锥B-EFC的体积.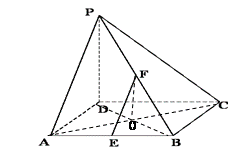
 中,
中,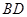 和平面
和平面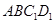 所成角的大小是( )
所成角的大小是( )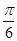
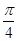
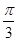
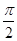
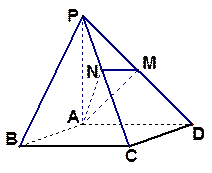
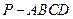 的底面是正方形,
的底面是正方形,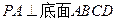 ,且
,且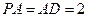 ,点
,点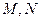 分别在侧棱
分别在侧棱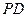 、
、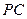 上,且
上,且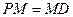 。
。
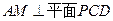 ;
;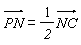 ,求平面
,求平面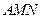 与平面
与平面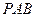 所成二面角的余弦值.
所成二面角的余弦值.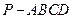 ,底面
,底面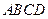 是边长为2的正方形,
是边长为2的正方形,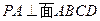 ,
,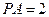 ,过点
,过点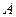 作
作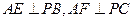 ,连接
,连接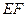 .
.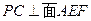 .
.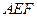 交侧棱
交侧棱 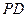 于点
于点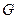 ,求多面体
,求多面体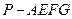 的体积。
的体积。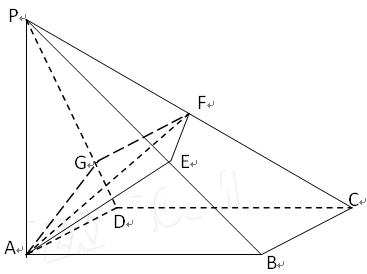
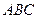 —
—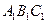 中,若∠BAC=
中,若∠BAC= ,
,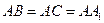 ,则异面直线
,则异面直线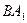 与
与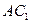 所成的角等于_________
所成的角等于_________