题目内容
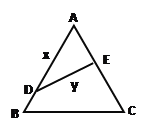
【题目】如图,已知![]() 是
是![]() 内角
内角![]() 的角平分线.
的角平分线.

(1)用正弦定理证明: ![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据![]() 是
是![]() 的角平分线,利用正弦定理,即可证明结论成立;
的角平分线,利用正弦定理,即可证明结论成立;
(2)根据余弦定理,先求出![]() 的值,再利用角平分线和余弦定理,即可求出
的值,再利用角平分线和余弦定理,即可求出![]() 的长.
的长.
试题解析:
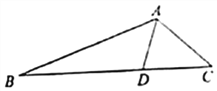
(1)∵AD是∠BAC的角平分线,∴∠BAD=∠CAD
根据正弦定理,在△ABD中,![]() =
=![]()
在△ADC中,![]() =
=![]()
∵sin∠ADB=sin(π﹣∠ADC)=sin∠ADC
∴![]() =
=![]() ,
,![]() =
=![]()
∴![]() =
=![]()
(2)根据余弦定理,cos∠BAC=![]()
即cos120°=![]()
解得BC=![]()
又![]() =
=![]()
∴![]() =
=![]() ,
,
解得CD=![]() ,BD=
,BD=![]() ;
;
设AD=x,则在△ABD与△ADC中,
根据余弦定理得,
cos60°=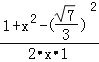
且cos60°=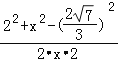
解得x=![]() ,即AD的长为
,即AD的长为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目