题目内容
3.已知集合A={x|ax2-(a+a2)x+a2>0}.(1)当常数a∈R,求集合A;
(2)在(1)的结论下,若B={x|1<x<a2-1}且A∩B=∅,求实数a的取值范围.
分析 (1)ax2-(a+a2)x+a2=a[x2-(1+a)x+a],解x2-(1+a)x+a得:x=1,或x=a;对a值分类讨论,可得不同情况下的集合A;
(2)当A=∅,或B=∅时,满足A∩B=∅;当A≠∅,且B≠∅时,若A∩B=∅,则集合A,B没有公共元素,分灶讨论各种情况下实数a的取值范围,最后综合讨论结果,可得答案.
解答 解:(1)∵ax2-(a+a2)x+a2=a[x2-(1+a)x+a],
解x2-(1+a)x+a得:x=1,或x=a;
当a>1时,集合A={x|ax2-(a+a2)x+a2>0}={x|x<1,或x>a},
当a=1时,集合A={x|ax2-(a+a2)x+a2>0}={x|x<1,或x>1},
当0<a<1时,集合A={x|ax2-(a+a2)x+a2>0}={x|x<a,或x>1},
当a=0时,集合A=∅,
当a<0时,集合A={x|ax2-(a+a2)x+a2>0}={x|a<x<1}
(2)当-$\sqrt{2}$≤a≤$\sqrt{2}$时,a2-1≤1,此时B=∅,满足A∩B=∅,
当a<$-\sqrt{2}$时,A={x|a<x<1},满足A∩B=∅,
当a$>\sqrt{2}$时,集合A={x|x<1,或x>a},
若A∩B=∅,则a≥a2-1,解得:$\frac{1-\sqrt{5}}{2}$<a<$\frac{1+\sqrt{5}}{2}$,
故$\sqrt{2}$<a<$\frac{1+\sqrt{5}}{2}$,
综上所述,a<$\frac{1+\sqrt{5}}{2}$
点评 本题考查的知识点是二次不等式的解法,集合的交集,分类讨论思想,难度中档.

练习册系列答案
相关题目
13.设a2<b2,a-b>0,则( )
| A. | b<0 | B. | b>0 | C. | a<0 | D. | a>0 |
15.某办公室有男职工5人,女职工4人,欲从中抽调3人支援其他工作,但至少要有2位是男士,则抽凋方案有( )种.
| A. | 18 | B. | 30 | C. | 40 | D. | 50 |
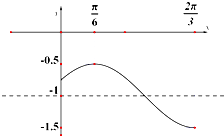 如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.
如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.