题目内容
14.函数f(x)=(|x|-1)(x+a)为奇函数,则a=0,f(x)减区间为$[-\frac{1}{2},\frac{1}{2}]$.分析 根据题意求出函数的定义域,利用奇函数的结论:f(0)=0,列出方程求出a的值,再化简函数解析式,由二次函数的图象画出函数的图象,再求出函数的减区间.
解答 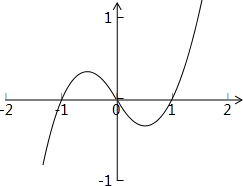 解:因为f(x)的定义域是R,且f(x)是奇函数,所以f(0)=0,
解:因为f(x)的定义域是R,且f(x)是奇函数,所以f(0)=0,
则f(0)=(0-1)(0+a)=-a=0,解得a=0,
所以f(x)=x(|x|-1)=$\left\{\begin{array}{l}{{x}^{2}-x,x≥0}\\{-{x}^{2}-x,x<0}\end{array}\right.$,
在坐标系中画出函数的图象:
由图可得,函数f(x)的减区间是$[-\frac{1}{2},\frac{1}{2}]$,
故答案为:0;$[-\frac{1}{2},\frac{1}{2}]$.
点评 本题考查奇函数的结论:f(0)=0的应用,以及分段函数的单调性,注意奇函数在原点有意义才能用此结论,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.若方程($\frac{1}{4}$)x+($\frac{1}{2}$x-1+a=0)有正数解,则实数a的取值范围是( )
| A. | 0<a<1 | B. | -3<a<0 | C. | -2<a<0 | D. | -1<a<0 |
5.已知等比数列{an}前n项和为Sn,且a2015=3S2014+2015,a2014=3S2013+2015,则公比q等于( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 4 | D. | $\frac{1}{4}$ |
2.在3x+2y<6表示的平面区域内的一个点是( )
| A. | (3,0) | B. | (1,3) | C. | (0,3) | D. | (0,0) |
9.已知f(x)=3sinx-πx,对任意的x∈(0,$\frac{π}{2}$),给出以下四个结论:
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
①f′(x)>0;
②f′(x)<0;
③f(x)>0;
④f(x)<0.
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
19.已知集合M=|x|x2-2x<0|,N=|x|x>1|,则M∩∁RN=( )
| A. | [1,2) | B. | (1,2) | C. | [0,1) | D. | (0,1] |
6.已知a、b、c分别为△ABC三个内角A,B,C的对边,若A=$\frac{π}{3}$,则a(cosC+$\sqrt{3}$sinC)=( )
| A. | a+b | B. | b+c | C. | a+c | D. | a+b+c |
3.设全集U=R,A={x||x|<2},B={x|y=$\sqrt{x-1}$},则图中阴影部分所表示的集合( )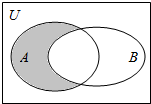

| A. | (-2,+∞) | B. | (1,2] | C. | (-2,1) | D. | (-2,1] |