题目内容
5.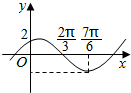 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一部分图象如图所示.(1)求函数f(x)的解析式;
(2)若函数g(x)=3[f(x)]2-f(x)+m在(-$\frac{π}{3}$,$\frac{2π}{3}$)内有两个不同的零点,求实数m的取值范围.
分析 (1)利用由y=Asin(ωx+φ)的部分图象可求得A,T,从而可得ω,又曲线经过($\frac{2π}{3}$,0),|φ|<$\frac{π}{2}$,可得φ的值,从而可求函数f(x)的解析式;
(2)由函数的定义域求出该三角函数与二次函数复合的函数的值域.
解答 解:(1)解:由图知A=2,T=4($\frac{7π}{6}$-$\frac{2π}{3}$)=2π,
∴ω=$\frac{2π}{2π}$=1,
∴f(x)=2sin(x+φ),
∵f($\frac{2π}{3}$)=0,
∴$\frac{2π}{3}$+φ=kπ,k∈Z.
∴φ=kπ-$\frac{2π}{3}$,k∈Z.
又|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{3}$,
∴函数f(x)的解析式为:f(x)=2sin(x+$\frac{π}{3}$).
(2)∵x∈(-$\frac{π}{3}$,$\frac{2π}{3}$),
∴2sin(x+$\frac{π}{3}$)∈(0,2]
又m=-3[f(x)]2+f(x),
∴而f(x)=2sin(x+$\frac{π}{3}$)∈(0,2],
则m∈(-10,$\frac{1}{12}$).
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求φ的值是关键,也是难点,考查识图与运算求解能力,此外还考查了已知三角函数的定义域求出由三角函数与二次函数复合的函数的值域,属于基本知识的考查.

练习册系列答案
相关题目
13.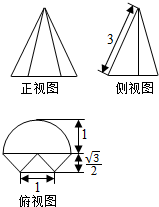 一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
 一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )| A. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |
10.在△ABC中,AC=20,∠A=90°,S△ABC=120,则AB=( )
| A. | 6 | B. | 12 | C. | 24 | D. | 3 |