题目内容
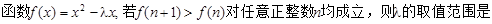 ( )
( )A.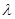 >0 >0 | B.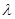 >-3 >-3 | C.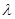 <1 <1 | D.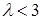 |
D
试题分析:方法一:由
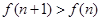 ,可得
,可得 ,化简得
,化简得 ,要使对于任意正整数n都成立,则
,要使对于任意正整数n都成立,则 ,即
,即 .
.方法二:因
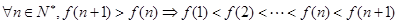 ,则
,则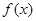 在
在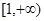 上为单调递增函数,但考虑到
上为单调递增函数,但考虑到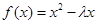 为二次函数,且单调性只需满足整数点,所以二次函数的对称轴
为二次函数,且单调性只需满足整数点,所以二次函数的对称轴 (满足
(满足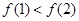 ,而不是对称轴
,而不是对称轴 ),解得
),解得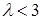 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
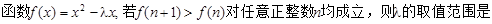 ( )
( )A.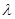 >0 >0 | B.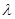 >-3 >-3 | C.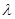 <1 <1 | D.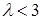 |
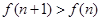 ,可得
,可得 ,化简得
,化简得 ,要使对于任意正整数n都成立,则
,要使对于任意正整数n都成立,则 ,即
,即 .
.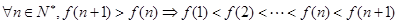 ,则
,则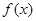 在
在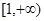 上为单调递增函数,但考虑到
上为单调递增函数,但考虑到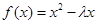 为二次函数,且单调性只需满足整数点,所以二次函数的对称轴
为二次函数,且单调性只需满足整数点,所以二次函数的对称轴 (满足
(满足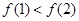 ,而不是对称轴
,而不是对称轴 ),解得
),解得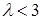 .
.
 名校课堂系列答案
名校课堂系列答案