题目内容
对于任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,那么x的取值范围是( )
| A.(1,3) | B.(-∞,1)∪(3,+∞) |
| C.(1,2) | D.(3,+∞) |
B
f(x)=x2+(a-4)x+4-2a=(x-2)a+x2-4x+4,
令g(a)=(x-2)a+x2-4x+4,
由题意知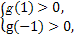 即
即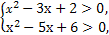
解得x>3或x<1,故选B.
令g(a)=(x-2)a+x2-4x+4,
由题意知
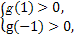 即
即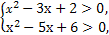
解得x>3或x<1,故选B.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
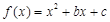 ,其中
,其中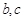 为常数.
为常数. 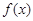 在区间
在区间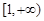 上单调,求
上单调,求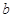 的取值范围;
的取值范围;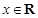 ,都有
,都有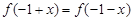 成立,且函数
成立,且函数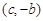 ,
, (a>0,a≠1)
(a>0,a≠1) 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.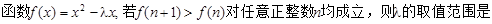 ( )
( )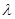 >0
>0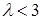
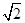
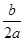
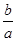
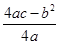
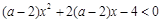 对一切
对一切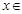 R恒成立,则实数
R恒成立,则实数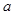 的取值范围是( )
的取值范围是( )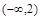
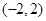

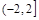
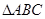 中,
中,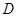 是
是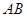 的中点,
的中点,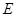 为线段
为线段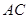 上一动点,则
上一动点,则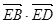 的取值范
的取值范