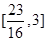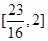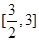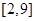题目内容
已知a∈(0,+∞),函数f(x)=ax2+2ax+1,若f(m)<0,比较大小:f(m+2)________1(用“<”“=”或“>”连接).
>
由f(x)=ax2+2ax+1(a>0)知f(x)过定点(0,1).又f(x)=ax2+2ax+1=a(x+1)2-a+1(a>0),设f(x)=0的两个实数根为x1,x2,且x1<x2,如图所示.所以x1+x2=-2,x1x2=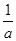 ,由Δ>0得a>1,所以x2-x1=
,由Δ>0得a>1,所以x2-x1=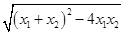 =
=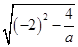 ∈(0,2).
∈(0,2).
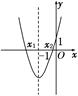
又因为对称轴为直线x=-1,f(0)=1,
所以x2∈(-1,0).
由f(m)<0,得x1<m<x2,
所以m+2>0,所以f(m+2)>1.
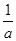 ,由Δ>0得a>1,所以x2-x1=
,由Δ>0得a>1,所以x2-x1=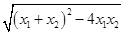 =
=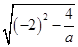 ∈(0,2).
∈(0,2).
又因为对称轴为直线x=-1,f(0)=1,
所以x2∈(-1,0).
由f(m)<0,得x1<m<x2,
所以m+2>0,所以f(m+2)>1.

练习册系列答案
相关题目
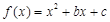 ,其中
,其中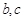 为常数.
为常数. 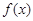 在区间
在区间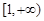 上单调,求
上单调,求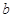 的取值范围;
的取值范围;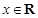 ,都有
,都有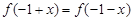 成立,且函数
成立,且函数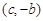 ,
,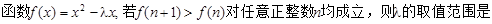 ( )
( )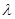 >0
>0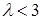
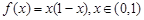 的最大值为_________
的最大值为_________



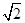
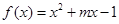 ,若对于任意的
,若对于任意的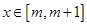 都有
都有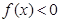 ,则实数
,则实数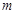 的取值范围为 .
的取值范围为 .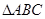 中,
中,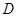 是
是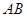 的中点,
的中点,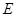 为线段
为线段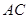 上一动点,则
上一动点,则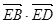 的取值范
的取值范