Question

【题目】从某校高一年级学生中随机抽取了20名学生，将他们的数学检测成绩（分）分成六段（满分100分，成绩均为不低于40分的整数）：，，...，后，得到如图所示的频率分布直方图.

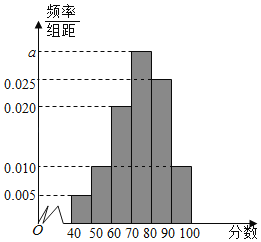
（Ⅰ）求图中实数的值；

（Ⅱ）若该校高一年级共有学生600名，试根据以上数据，估计该校高一年级数学检测成绩不低于80分的人数.

Answer 1

【答案】（Ⅰ）；（Ⅱ）210.

【解析】

（Ⅰ）由等比数列性质及频率分布直方图，列出方程，能求出．

（Ⅱ）利用频率分布直方图能求出成绩不低于80分的人数．

解：（Ⅰ）因为图中所有小矩形的面积之和等于1，

所以，

解得.

（Ⅱ）根据频率分布直方图，成绩不低于80分的频率为

.

由于该校高一年级共有学生600名，利用样本估计总体的思想，可估计该校高一年级数学检测成绩不低于80分的人数为.