题目内容
20.甲乙两位同学约定早上7点至12点之间在某地会面,先到者等一个小时后即离去.设两人在这段时间内的各时刻到达是等可能的,且二人互不影响,则二人能会面的概率为$\frac{9}{25}$.分析 由题意知本题是一个几何概型,试验发生包含的所有事件对应的集合是Ω={(x,y)|0<x<5,0<y<5}做出集合对应的面积是边长为5的正方形的面积,写出满足条件的事件对应的集合和面积,根据面积之比得到概率
解答  解:由题意知本题是一个几何概型,
解:由题意知本题是一个几何概型,
∵试验发生包含的所有事件对应的集合是Ω={(x,y)|0<x<5,0<y<5}
集合对应的面积是边长为5的正方形的面积s=25,
而满足条件的事件对应的集合是A═{(x,y)|0<x<5,0<y<5,|x-y|≤1}
得到sA=9
∴两人能够会面的概率是$\frac{9}{25}$;
故答案为:$\frac{9}{25}$.
点评 本题考查了几何概型;解答本题的难点是把时间分别用x,y坐标来表示,从而把时间长度这样的一维问题转化为平面图形的二维面积问题,转化成面积型的几何概型问题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.已知{an}的通项an=23-n,则a1a2+a2a3+…+anan+1=( )
| A. | $\frac{32}{3}$(1-4-n) | B. | $\frac{32}{3}$(1-2-n) | C. | 16(1-4-n) | D. | 16(1-2-n) |
15.偶函数f(x)=loga|x+b|在(-∞,0)上单调递减,则f(a+1)与f(2-b)的大小关系是( )
| A. | f(a+1)>f(2-b) | B. | f(a+1)=f(2-b) | C. | f(a+1)<f(2-b) | D. | 不能确定 |
11.设等差数列{an}的前n项和为Sn,且满足S2014>0,S2015<0,对任意正整数n,都有|an|≥|ak|,则k的值为( )
| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
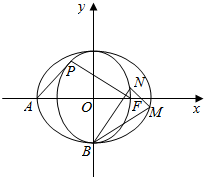 已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.
已知椭圆C1:$\frac{{x}^{2}}{2}$+y2=1和圆C2:x2+y2=1,A,B,F分别为椭圆C1左顶点、下顶点和右焦点.