Question

12．设f（x）是定义在（-∞，+∞）上的以2为周期的周期函数且f（x）为偶函数，在区间[2，3]上，f（x）=-2（x-3）²+4．
（1）当x∈[1，2]时，f（x）的解析式；
（2）若矩形ABCD的两个顶点A、B在x轴上，C、D在y=f（x）（0≤x≤2）的图象上，求这个矩形面积的值．

Answer 1

分析 （1）当x∈[-3，-2]时-x∈[2，3]，利用偶函数的性质求出f（x），再利用函数的周期性求出x∈[1，2]的f（x）解析式；
（2）利用函数的周期性求出x∈[0，1]上的解析式，由（1）可得在[0，2]上的解析式，由二次函数的性质和题意设两顶点C、D的坐标，根据矩形面积公式代入求出S，再利用导数判断出函数的单调性和极值，再求其最大值即可．

解答 解：（1）当x∈[-3，-2]时，-x∈[2，3]，
∵f（x）是偶函数，在区间[2，3]上，f（x）=-2（x-3）²+4，
∴f（x）=f（-x）=-2（-x-3）²+4=-2（x+3）²+4．
当x∈[1，2]时，-3≤x-4≤-2，∵f（x）是以2为周期的周期函数，
∴f（x）=f（x-4）=-2[（x-4）+3]²+4=-2（x-1）²+4．
∴f（x）=-2（x-1）²+4（1≤x≤2）；
（2）当x∈[0，1]时，2≤x+2≤3，∵f（x）是以2为周期的周期函数，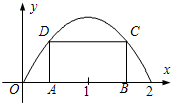
∴f（x）=f（x+2）=-2[（x+2）-3]²+4=-2（x-1）²+4．
∴f（x）=-2（x-1）²+4（0≤x≤1），
由（1）知，f（x）=-2（x-1）²+4（0≤x≤2），如右图：
设D（x，t），C（2-x，t），则t=-2（x-1）²+4，
∴矩形ABCD的面积S（x）=|AB|×|BC|=（2-2x）t=（2-2x）（-2x²+4x+2）
=4（x³-3x²+x+1），
则S′（x）=4（3x²-6x+1），由S′=4（3x²-6x+1）=0得，
${x}_{1}=\frac{3-\sqrt{6}}{3}$＞0，${x}_{2}=\frac{3+\sqrt{6}}{3}$＜2，
∴当x＞$\frac{3+\sqrt{6}}{3}$或x＜$\frac{3-\sqrt{6}}{3}$时，f′（x）＞0；当$\frac{3-\sqrt{6}}{3}$＜x＜$\frac{3+\sqrt{6}}{3}$时，f′（x）＜0，
则S（x）在（0，$\frac{3-\sqrt{6}}{3}$）、（$\frac{3+\sqrt{6}}{3}$，2）为增函数，在（$\frac{3-\sqrt{6}}{3}$，$\frac{3+\sqrt{6}}{3}$）为减函数，
∴S（x）在x=$\frac{3-\sqrt{6}}{3}$处取得极大值也是最大值，
∵S（$\frac{3-\sqrt{6}}{3}$）=（2-2×$\frac{3-\sqrt{6}}{3}$）[-2×$（\frac{3-\sqrt{6}}{3}）^{2}$+4×$\frac{3-\sqrt{6}}{3}$+2]=$\frac{2\sqrt{6}}{3}×\frac{8}{3}$=$\frac{16\sqrt{6}}{9}$，
∴S（x）_max=$\frac{16\sqrt{6}}{9}$，
综上可得，这个矩形面积的最大值是$\frac{16\sqrt{6}}{9}$．

点评 本题考查利用函数的奇偶性、周期性求函数的解析式，导数与函数的单调性、极值和最值的关系，此题是一道中档题，计算量比较大，考查学生的计算能力．