题目内容
1.已知向量$\overrightarrow a=(cos\frac{3x}{2},\;\;sin\frac{3x}{2})$,$\overrightarrow b=(cos\frac{x}{2},\;\;-sin\frac{x}{2})$,其中x∈R.(1)当$\overrightarrow a⊥\overrightarrow b$时,求x值的集合;
(2)当$\overrightarrow a∥$$\overrightarrow b$时,求x值的集合.
分析 (1)由$\overrightarrow a⊥\overrightarrow b$,得$\overrightarrow{a}•\overrightarrow{b}$=0,由三角函数中的恒等变换应用可得cos2x=0,由余弦函数的性质即可求得x值的集合;
(2)由$\overrightarrow a∥\overrightarrow b$,得$cos\frac{x}{2}sin\frac{3x}{2}+sin\frac{x}{2}cos\frac{3x}{2}=0$,由三角函数中的恒等变换应用可得sin2x=0,由正弦函数的性质即可求得x值的集合.
解答 解:(1)由$\overrightarrow a⊥\overrightarrow b$,得$\overrightarrow{a}•\overrightarrow{b}$=0,即$cos\frac{3x}{2}cos\frac{x}{2}-sin\frac{3x}{2}sin\frac{x}{2}=0$.…(4分)
则cos2x=0,得$x=\frac{kπ}{2}+\frac{π}{4}(k∈{Z})$. …(5分)
∴$\left\{{x|x=\frac{kπ}{2}+\frac{π}{4},k∈Z}\right\}$为所求. …(6分)
(2)由$\overrightarrow a∥\overrightarrow b$,得$cos\frac{x}{2}sin\frac{3x}{2}+sin\frac{x}{2}cos\frac{3x}{2}=0$…(10分)
则sin2x=0,得$x=\frac{kπ}{2}(k∈{Z})$.…(11分)
∴$\left\{{x|x=\frac{kπ}{2},k∈Z}\right\}$为所求.…(12分)
点评 本题主要考查了三角函数中的恒等变换应用,平面向量共线(平行)的坐标表示,三角函数的图象和性质,属于基本知识的考查.

| A. | $y=sin(-2x-\frac{2π}{3})$ | B. | $y=sin(-2x+\frac{2π}{3})$ | C. | $y=sin(-2x-\frac{π}{3})$ | D. | $y=sin(-2x+\frac{π}{3})$ |
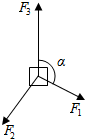 如图,一物体在水平面内的三个力F1、F2、F3的作用下保持平衡,如果F1=5N,F2=7N,∠α=120°,则F3=8N.
如图,一物体在水平面内的三个力F1、F2、F3的作用下保持平衡,如果F1=5N,F2=7N,∠α=120°,则F3=8N.