题目内容

2．观察数列1，3，7，15，31，…，归纳出该数列的一个通项公式an=2n-1．

分析 由数列1，3，7，15，31，…，可得：a1=21-1，a2=22-1，a3=23-1，…，即可得出．

解答 解：由数列3、5、9、17、33…可得：
a1=21-1，a2=22-1，a3=23-1，…，
可得：an=2n-1．
故答案为：2n-1．

点评 本题考查了通过观察分析猜想归纳求数列的通项公式，注意2n的应用，属于基础题．

练习册系列答案
相关题目
1．已知向量$\overrightarrow a=（cos\frac{3x}{2}，\;\;sin\frac{3x}{2}）$，$\overrightarrow b=（cos\frac{x}{2}，\;\;-sin\frac{x}{2}）$，其中x∈R．
（1）当$\overrightarrow a⊥\overrightarrow b$时，求x值的集合；　　
（2）当$\overrightarrow a∥$$\overrightarrow b$时，求x值的集合．
13．全集U={0，1，2，3，5，6，8 }，集合A={ 1，5，8 }，B={ 2 }，则集合（∁UA）∪B为（　　）
A．{ 0，2，3，6 }B．{ 0，3，6 }C．{ 1，2，5，8 }D．∅
10．已知甲盒内有大小相同的1个红球和3个黑球，乙盒内有大小相同的2个红球和4个黑球．现从甲、乙两个盒内各任取2个球．
（1）求取出的4个球均为黑球的概率；
（2）求取出的4个球中恰有1个红球的概率；
（3）设ξ为取出的4个球中红球的个数，求ξ的分布列．
17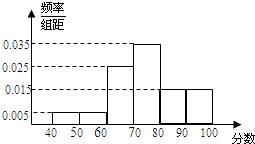．某校1000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示．则不低于60分的人数是（　　）
A．800B．900C．950D．990
7．如图，正三棱柱ABC-A1B1C1中，D是BC的中点AA1=AB=1
（1）求证：A1C∥平面AB1D
（2）求二面角B-AB1-D的余弦值．
14．（1）用二项式定理证明：32n-8n-1能被64整除（n∈N*）；
（2）求230-3除以7的余数．
11．已知y=a-bcos2x（b＞0）的最大值是$\frac{3}{2}$，最小值是-$\frac{1}{2}$，求函数y=-4asin（3bx+$\frac{π}{3}$）的周期、最大值及取得最大值时x的值的集合．
12．在等比数列{an}（n∈N*）中，若a1=1，a4=$\frac{1}{8}$，则该数列的前12项和为（　　）
A．2-$\frac{1}{{2}^{4}}$B．2-$\frac{1}{{2}^{2}}$C．2-$\frac{1}{{2}^{10}}$D．2-$\frac{1}{{2}^{11}}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网