题目内容
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.记CD=x,V(x)表示四棱锥F-ABCD的体积.
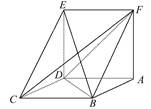
(1)求V(x)的表达式.
(2)求V(x)的最大值.

(1)求V(x)的表达式.
(2)求V(x)的最大值.
(1) V(x)=  x
x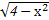 (0<x<2) (2)
(0<x<2) (2)
 x
x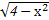 (0<x<2) (2)
(0<x<2) (2)
【思路点拨】利用体积公式得到V(x)的表达式,然后根据基本不等式或函数的知识求最大值.
解:(1)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x,
∴FA=2,BD=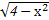 (0<x<2),
(0<x<2),
∴S?ABCD=CD·BD=x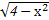 ,
,
∴V(x)= S?ABCD·FA=
S?ABCD·FA= x
x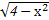 (0<x<2).
(0<x<2).
(2)方法一:要使V(x)取得最大值,只需x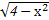 =
=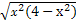 (0<x<2)取得最大值,
(0<x<2)取得最大值,
∵x2(4-x2)≤(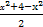 )2=4,
)2=4,
∴V(x)≤ ×2=
×2= .
.
当且仅当x2=4-x2,即x=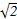 时等号成立.
时等号成立.
故V(x)的最大值为 .
.
方法二:V(x)= x
x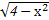 =
=
= .
.
∵0<x<2,∴0<x2<4,∴当x2=2,即x=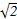 时,V(x)取得最大值,且V(x)max=
时,V(x)取得最大值,且V(x)max= .
.
解:(1)∵平面ADEF⊥平面ABCD,交线为AD且FA⊥AD,∴FA⊥平面ABCD.
∵BD⊥CD,BC=2,CD=x,
∴FA=2,BD=
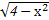 (0<x<2),
(0<x<2),∴S?ABCD=CD·BD=x
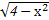 ,
,∴V(x)=
 S?ABCD·FA=
S?ABCD·FA= x
x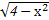 (0<x<2).
(0<x<2).(2)方法一:要使V(x)取得最大值,只需x
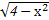 =
=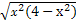 (0<x<2)取得最大值,
(0<x<2)取得最大值,∵x2(4-x2)≤(
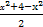 )2=4,
)2=4,∴V(x)≤
 ×2=
×2= .
.当且仅当x2=4-x2,即x=
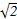 时等号成立.
时等号成立.故V(x)的最大值为
 .
.方法二:V(x)=
 x
x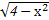 =
=
=
 .
.∵0<x<2,∴0<x2<4,∴当x2=2,即x=
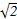 时,V(x)取得最大值,且V(x)max=
时,V(x)取得最大值,且V(x)max= .
.
练习册系列答案
相关题目
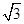 ,AB=2CD=8.
,AB=2CD=8.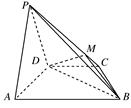
 为圆
为圆 的直径,点
的直径,点 .
.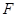 在圆
在圆 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
.
 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; 的体积.
的体积.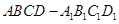 的8个顶点都在球
的8个顶点都在球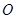 的表面上,
的表面上,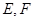 分别是棱
分别是棱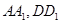 的中点,点
的中点,点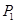 ,
,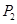 分别是线段
分别是线段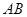 ,
,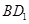 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段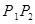 平行于平面
平行于平面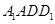 ,则
,则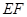 被球
被球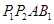 的体积的最大值是
的体积的最大值是 π
π 所在平面与矩形
所在平面与矩形 所在平面互相垂直,
所在平面互相垂直, ,
, ,若点
,若点 都在同一球面上,则此球的表面积等于 .
都在同一球面上,则此球的表面积等于 . ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.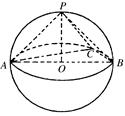
 ,高为
,高为 的正三棱锥的全面积为
的正三棱锥的全面积为  .
.