题目内容
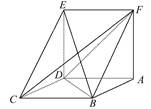
棱长为1的正方体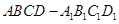 的8个顶点都在球
的8个顶点都在球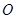 的表面上,
的表面上,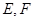 分别是棱
分别是棱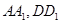 的中点,点
的中点,点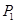 ,
,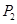 分别是线段
分别是线段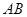 ,
,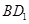 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段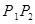 平行于平面
平行于平面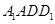 ,则
,则
(1)直线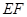 被球
被球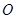 截得的线段长为
截得的线段长为
(2)四面体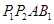 的体积的最大值是
的体积的最大值是
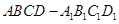 的8个顶点都在球
的8个顶点都在球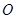 的表面上,
的表面上,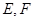 分别是棱
分别是棱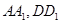 的中点,点
的中点,点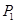 ,
,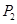 分别是线段
分别是线段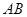 ,
,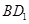 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段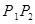 平行于平面
平行于平面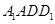 ,则
,则(1)直线
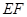 被球
被球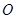 截得的线段长为
截得的线段长为(2)四面体
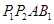 的体积的最大值是
的体积的最大值是(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)因为点
 在圆上,
在圆上,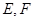 为中点,所以直线
为中点,所以直线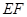 被球
被球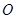 截得的线段长为正方形
截得的线段长为正方形 的外接圆直径,等于
的外接圆直径,等于 ,(2)过
,(2)过 做
做 与
与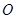 点,连接
点,连接 ∵
∵ ,
, ,
,
 平面
平面 ∥平面
∥平面 ,
, 为平面
为平面 与两平行平面的交线,
与两平行平面的交线, ,又
,又 ,
, ,
, 平面
平面 ,
,设正方体的棱长为1,
 ,则
,则 ,
,
当
 时,最大值为
时,最大值为 .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高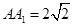 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点. 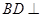 平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.
 中,侧棱
中,侧棱 平面
平面 ,
,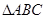 为等腰直角三角形,
为等腰直角三角形, ,且
,且 分别是
分别是 的中点.
的中点.
 平面
平面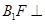 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为 靠近
靠近 的三等分点,点
的三等分点,点 为边
为边 边的中点,线段
边的中点,线段 交线段
交线段 于点
于点 .将
.将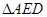 沿
沿 平面
平面 ,连接
,连接 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.
 平面
平面
 的体积.
的体积. 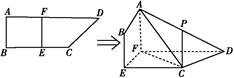
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
 的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12
的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12 ,则该三棱柱的体积为.
,则该三棱柱的体积为. 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )