题目内容
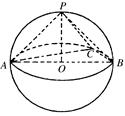
已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心O在AB上,PO⊥平面ABC, ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.
 ,则三棱锥与球的体积之比为________.
,则三棱锥与球的体积之比为________.
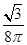
依题意,AB=2R,又 ,∠ACB=90°,因此AC=
,∠ACB=90°,因此AC=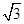 R,BC=R,三棱锥P-ABC的体积VP-ABC=
R,BC=R,三棱锥P-ABC的体积VP-ABC=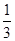 PO·S△ABC=
PO·S△ABC=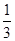 ×R×
×R×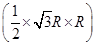 =
=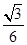 R3.
R3.
而球的体积V球=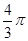 R3,因此VP-ABC∶V球=
R3,因此VP-ABC∶V球=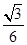 R3∶
R3∶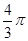 R3=
R3=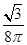 .
.
 ,∠ACB=90°,因此AC=
,∠ACB=90°,因此AC=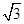 R,BC=R,三棱锥P-ABC的体积VP-ABC=
R,BC=R,三棱锥P-ABC的体积VP-ABC=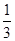 PO·S△ABC=
PO·S△ABC=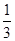 ×R×
×R×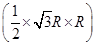 =
=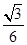 R3.
R3.而球的体积V球=
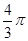 R3,因此VP-ABC∶V球=
R3,因此VP-ABC∶V球=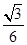 R3∶
R3∶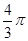 R3=
R3=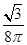 .
.
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
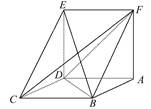
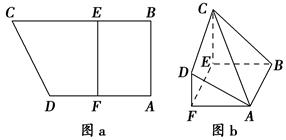
 是边长为6的等边三角形,
是边长为6的等边三角形, 分别为
分别为 靠近
靠近 的三等分点,点
的三等分点,点 为边
为边 边的中点,线段
边的中点,线段 交线段
交线段 于点
于点 .将
.将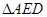 沿
沿 平面
平面 ,连接
,连接 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.
 平面
平面
 的体积.
的体积. 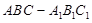 中,
中,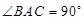 ,
,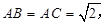
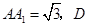 是
是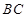 中点,
中点,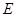 是
是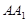 中点.
中点.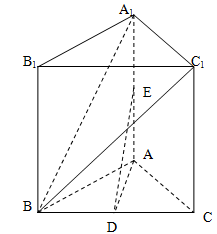
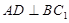 ;
;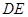 ∥面
∥面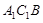 .
.
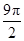 ,则正方体的棱长为 .
,则正方体的棱长为 .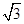 的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为
的正三角形,侧棱垂直于底面,且该三棱柱的外接球的体积为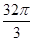 ,则该三棱柱的体积为________.
,则该三棱柱的体积为________.