题目内容
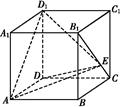
已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把△ACD折起,则三棱锥外接球表面积等于( )
| A.8π | B.16π | C.48 π π | D.50π |
B
设矩形长为x,则宽为 (x>0),
(x>0),
周长P=2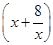 ≥2·2
≥2·2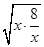 =8
=8 .
.
当且仅当x= ,
,
即x=2 时,周长取到最小值.
时,周长取到最小值.
此时正方形ABCD沿AC折起,取AC的中点为O,则
OA=OB=OC=OD,
三棱锥D ABC的四个顶点都在以O为球心,以2为半径的球上,此球的表面积为4π·22=16π.
ABC的四个顶点都在以O为球心,以2为半径的球上,此球的表面积为4π·22=16π.
 (x>0),
(x>0),周长P=2
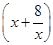 ≥2·2
≥2·2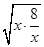 =8
=8 .
.当且仅当x=
 ,
,即x=2
 时,周长取到最小值.
时,周长取到最小值.此时正方形ABCD沿AC折起,取AC的中点为O,则
OA=OB=OC=OD,
三棱锥D
 ABC的四个顶点都在以O为球心,以2为半径的球上,此球的表面积为4π·22=16π.
ABC的四个顶点都在以O为球心,以2为半径的球上,此球的表面积为4π·22=16π.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
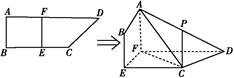
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
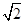 ,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.
,E为CD的中点,将△BCE沿BE折起,使得CO⊥DE,其中垂足O在线段DE内.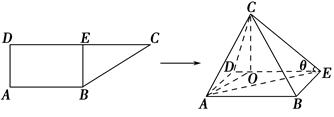
 的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12
的正三角形,侧棱垂直于底面,且该三棱柱的外接球表面积为12 ,则该三棱柱的体积为.
,则该三棱柱的体积为.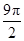 ,则正方体的棱长为 .
,则正方体的棱长为 .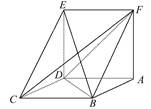
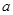 ,点
,点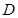 是
是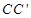 上任意一点,连接
上任意一点,连接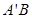 ,
,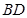 ,
,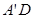 ,
,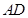 ,则三棱锥
,则三棱锥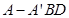 的体积为( )
的体积为( )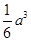
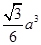

 A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A
A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A