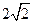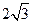题目内容
20.(本小题满分14分)
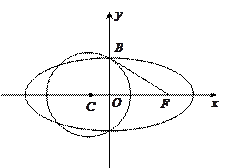
已知圆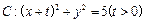 和椭圆
和椭圆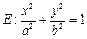
 的一个公共点为
的一个公共点为 .
. 为椭圆
为椭圆 的右焦点,直线
的右焦点,直线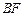 与圆
与圆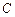 相切于点
相切于点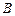 .
.
(Ⅰ)求 值和椭圆
值和椭圆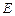 的方程;
的方程;
(Ⅱ)圆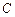 上是否存在点
上是否存在点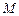 ,使
,使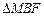 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点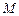 的坐标.
的坐标.
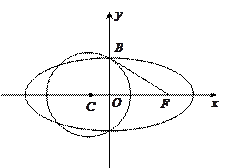
已知圆
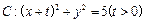 和椭圆
和椭圆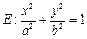
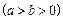 的一个公共点为
的一个公共点为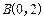 .
. 为椭圆
为椭圆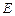 的右焦点,直线
的右焦点,直线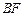 与圆
与圆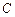 相切于点
相切于点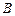 .
.(Ⅰ)求
 值和椭圆
值和椭圆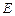 的方程;
的方程;(Ⅱ)圆
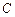 上是否存在点
上是否存在点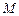 ,使
,使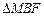 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点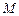 的坐标.
的坐标.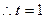 ,
,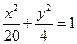 圆
圆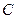 上存在点
上存在点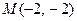 或
或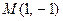 或
或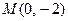 ,使
,使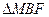
为等腰三角形.
20.解:(Ⅰ)由题可知,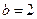 …………………………1分
…………………………1分
 ,
, ,
,

 ,又
,又 ,
,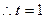 ……………………………3分
……………………………3分
法一: 为圆
为圆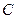 的切线,
的切线,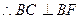 ,
, ,
,
设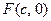 ,则有
,则有 ,
,
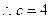 , …………………5分
, …………………5分
又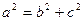 ,
, ,
, ,
,
所以椭圆 的方程为
的方程为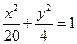 …………6分
…………6分
法二: 为圆
为圆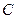 的切线,
的切线, ,
,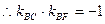 ,
,
设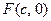 ,则有
,则有 ,
,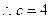 , …………………5分
, …………………5分
又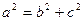 ,
, ,
, ,
, …………6分
…………6分
法三: 为圆
为圆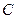 的切线,
的切线, 则圆心
则圆心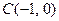 到直线
到直线 的距离等于
的距离等于 ,
,
又 ,
,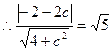 ,
,
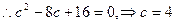 , ……………………………5分
, ……………………………5分
又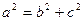 ,
, ,
, ,
, ……………6分
……………6分
(Ⅱ)法一:假设存在点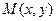 ,使
,使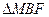 为等腰三角形,
为等腰三角形,
则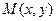 点满足
点满足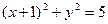 …………①, ………………7分
…………①, ………………7分
下面分三种情况讨论:
(1)当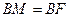 时,
时,
有 ,即
,即 …………②
…………②
由①②联立得: ,
, ……………………………9分
……………………………9分
(2)当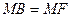 时,
时,
有 ,即
,即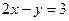 …………③
…………③
由①③联立得: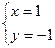 ,
, …………………………11分
…………………………11分
(3)当 时,
时,
有 ,即
,即 …………④
…………④
由①④联立得: ,又
,又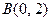 ,
, …………………13分
…………………13分
综上,圆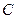 上存在点
上存在点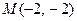 或
或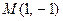 或
或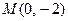 ,使
,使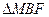
为等腰三角形. …………………14分
法二:假设存在点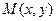 ,使
,使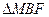 为等腰三角形,下面分三种情况讨论:
为等腰三角形,下面分三种情况讨论:
(1)当 时,
时,
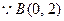 关于
关于 轴对称点
轴对称点 也在圆上,
也在圆上,
 ………………8分
………………8分
(2)当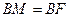 时,
时, ,
,
又圆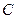 的直径为
的直径为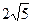 ,
,
 为圆
为圆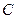 的直径,
的直径,
此时由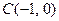 、
、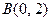 及中点公式得
及中点公式得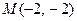 ; …………………11分
; …………………11分
(3)当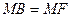 时,设
时,设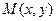 ,则有
,则有
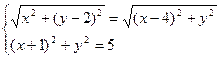
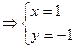 ,
, ………………………13分
………………………13分
综上,圆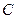 上存在点
上存在点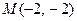 或
或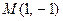 或
或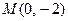 ,使
,使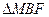
为等腰三角形. …………………………14分
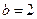 …………………………1分
…………………………1分 ,
, ,
,
 ,又
,又 ,
,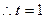 ……………………………3分
……………………………3分法一:
 为圆
为圆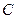 的切线,
的切线,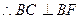 ,
, ,
,设
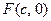 ,则有
,则有 ,
,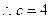 , …………………5分
, …………………5分又
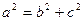 ,
, ,
, ,
,所以椭圆
 的方程为
的方程为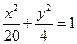 …………6分
…………6分法二:
 为圆
为圆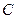 的切线,
的切线, ,
,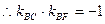 ,
,设
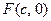 ,则有
,则有 ,
,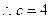 , …………………5分
, …………………5分又
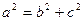 ,
, ,
, ,
, …………6分
…………6分法三:
 为圆
为圆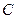 的切线,
的切线, 则圆心
则圆心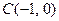 到直线
到直线 的距离等于
的距离等于 ,
,又
 ,
,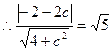 ,
,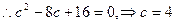 , ……………………………5分
, ……………………………5分又
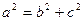 ,
, ,
, ,
, ……………6分
……………6分(Ⅱ)法一:假设存在点
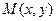 ,使
,使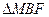 为等腰三角形,
为等腰三角形,则
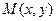 点满足
点满足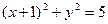 …………①, ………………7分
…………①, ………………7分下面分三种情况讨论:
(1)当
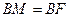 时,
时,有
 ,即
,即 …………②
…………②由①②联立得:
 ,
, ……………………………9分
……………………………9分(2)当
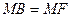 时,
时,有
 ,即
,即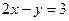 …………③
…………③由①③联立得:
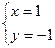 ,
, …………………………11分
…………………………11分(3)当
 时,
时,有
 ,即
,即 …………④
…………④由①④联立得:
 ,又
,又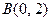 ,
, …………………13分
…………………13分综上,圆
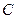 上存在点
上存在点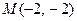 或
或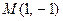 或
或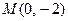 ,使
,使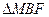
为等腰三角形. …………………14分
法二:假设存在点
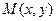 ,使
,使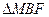 为等腰三角形,下面分三种情况讨论:
为等腰三角形,下面分三种情况讨论:(1)当
 时,
时,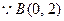 关于
关于 轴对称点
轴对称点 也在圆上,
也在圆上, ………………8分
………………8分(2)当
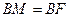 时,
时, ,
,又圆
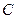 的直径为
的直径为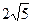 ,
,
 为圆
为圆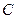 的直径,
的直径,此时由
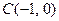 、
、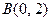 及中点公式得
及中点公式得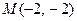 ; …………………11分
; …………………11分(3)当
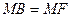 时,设
时,设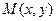 ,则有
,则有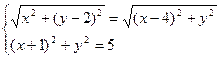
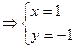 ,
, ………………………13分
………………………13分综上,圆
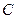 上存在点
上存在点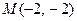 或
或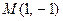 或
或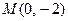 ,使
,使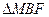
为等腰三角形. …………………………14分

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
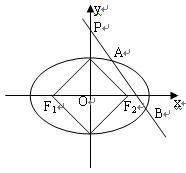
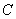 :
: 的左、右焦点分别为
的左、右焦点分别为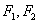 ,下顶点为
,下顶点为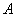 ,点
,点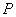 是椭圆上任一点,⊙
是椭圆上任一点,⊙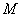 是以
是以 为直径的圆.
为直径的圆.
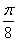 时,求
时,求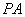 所在直线的方程;
所在直线的方程;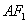 相切时,求⊙
相切时,求⊙
 的一个焦点
的一个焦点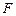 且垂直于
且垂直于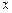 轴的直线交椭圆于点
轴的直线交椭圆于点 。
。 求椭圆C的方程;
求椭圆C的方程;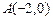 的直线
的直线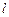 与椭圆
与椭圆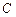 交于两点
交于两点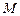 、
、 ,使得
,使得 (其中
(其中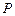 为弦
为弦 的中点)?若存在,求出直线
的中点)?若存在,求出直线
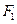 ,
, 分别是椭圆
分别是椭圆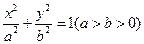 的左、右焦点,与直线
的左、右焦点,与直线 相切的
相切的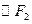 交椭圆于点
交椭圆于点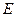 ,
,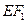 与
与 ,过椭圆的上顶点A的直线与
,过椭圆的上顶点A的直线与 ,求λ的取值范围.
,求λ的取值范围.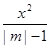 +
+ =1表示焦点在y轴上的椭圆,则m的取值范围是 ( )
=1表示焦点在y轴上的椭圆,则m的取值范围是 ( )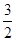
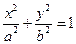
 的左焦点
的左焦点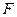 且倾斜角为
且倾斜角为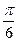 的直线被椭圆截得的弦长为
的直线被椭圆截得的弦长为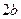 ,则离心率
,则离心率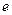 =_________
=_________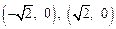 ,则PC·PD的最大值为 ( )
,则PC·PD的最大值为 ( ) C 3 D
C 3 D 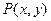 是椭圆
是椭圆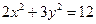 上的一个动点,则
上的一个动点,则 的最大值为( )
的最大值为( )