题目内容
(本小题12分)
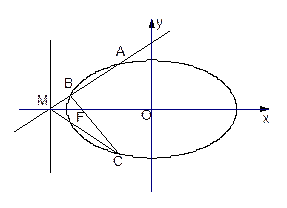
过椭圆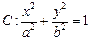
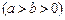 的一个焦点
的一个焦点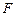 且垂直于
且垂直于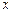 轴的直线交椭圆于点
轴的直线交椭圆于点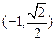 。
。
(Ⅰ) 求椭圆C的方程;
求椭圆C的方程;
(Ⅱ)是否存在过点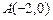 的直线
的直线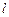 与椭圆
与椭圆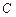 交于两点
交于两点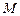 、
、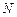 ,使得
,使得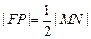 (其中
(其中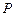 为弦
为弦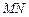 的中点)?若存在,求出直线
的中点)?若存在,求出直线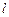 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
过椭圆
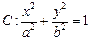
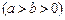 的一个焦点
的一个焦点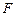 且垂直于
且垂直于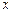 轴的直线交椭圆于点
轴的直线交椭圆于点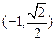 。
。(Ⅰ)
 求椭圆C的方程;
求椭圆C的方程;(Ⅱ)是否存在过点
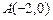 的直线
的直线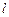 与椭圆
与椭圆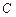 交于两点
交于两点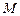 、
、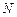 ,使得
,使得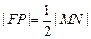 (其中
(其中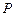 为弦
为弦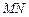 的中点)?若存在,求出直线
的中点)?若存在,求出直线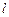 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
(Ⅰ) 椭圆
椭圆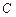 的方程为
的方程为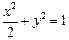
(Ⅱ) 满足条件的直线
满足条件的直线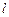 存在,方程为
存在,方程为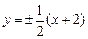
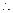 椭圆
椭圆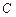 的方程为
的方程为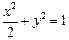
(Ⅱ)
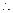 满足条件的直线
满足条件的直线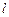 存在,方程为
存在,方程为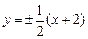
21.本小题主要考查直线、椭圆、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想.满分12分。
解:(I)依 题意,得
题意,得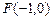
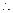
 . ………………………2分
. ………………………2分
解得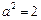 ,
,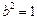 .
.
 椭圆
椭圆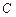 的方程为
的方程为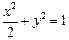 . ………………………4分
. ………………………4分
(注:本小题从椭圆定义求解亦可)
(II)设满足条件的直线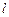 存在,方程为
存在,方程为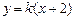 (
(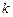 必
必 存在),代入椭圆方程,得
存在),代入椭圆方程,得
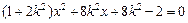 . ………………………5分
. ………………………5分
首先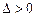 ,得
,得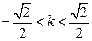 . ……………………6分
. ……………………6分
设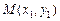 ,
,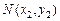 ,则
,则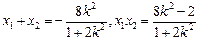 .……………………7分
.……………………7分

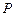 为
为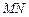 的中点,且
的中点,且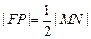 ,
,
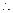
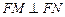 . ……………………8分
. ……………………8分
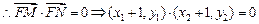

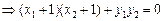
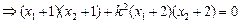
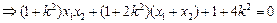
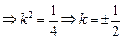 ,满足
,满足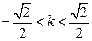 . ……………………11分
. ……………………11分
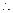 满足条件的直线
满足条件的直线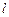 存在,方程为
存在,方程为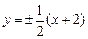 . ……………………12分
. ……………………12分
(注:考生对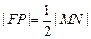 采用其它方法转化,可参照给分)
采用其它方法转化,可参照给分)
解:(I)依
 题意,得
题意,得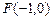
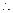
 . ………………………2分
. ………………………2分解得
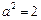 ,
,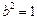 .
.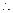 椭圆
椭圆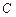 的方程为
的方程为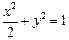 . ………………………4分
. ………………………4分(注:本小题从椭圆定义求解亦可)
(II)设满足条件的直线
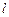 存在,方程为
存在,方程为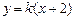 (
(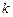 必
必 存在),代入椭圆方程,得
存在),代入椭圆方程,得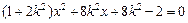 . ………………………5分
. ………………………5分首先
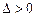 ,得
,得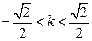 . ……………………6分
. ……………………6分设
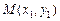 ,
,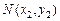 ,则
,则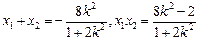 .……………………7分
.……………………7分
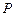 为
为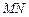 的中点,且
的中点,且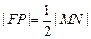 ,
,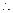
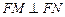 . ……………………8分
. ……………………8分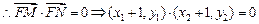

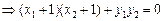
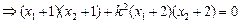
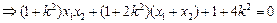
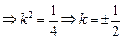 ,满足
,满足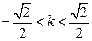 . ……………………11分
. ……………………11分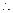 满足条件的直线
满足条件的直线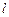 存在,方程为
存在,方程为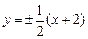 . ……………………12分
. ……………………12分(注:考生对
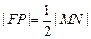 采用其它方法转化,可参照给分)
采用其它方法转化,可参照给分)
练习册系列答案
相关题目
 轴上,离心率为
轴上,离心率为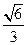 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为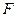 ,过左准线与
,过左准线与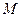 任作一条斜率不为零的直线
任作一条斜率不为零的直线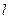 与椭圆W交于不同的两点
与椭圆W交于不同的两点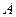 、
、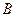 ,点
,点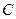 .
.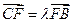 (
(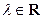 );
);
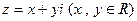 与复平面上点
与复平面上点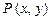 对应.
对应.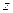 满足条件
满足条件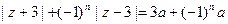 (其中
(其中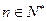 ,常数
,常数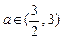 ),当
),当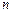 为奇数时,动点
为奇数时,动点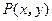 的轨迹为
的轨迹为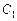 ;当
;当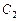 ,且两条曲线都经过点
,且两条曲线都经过点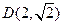 ,求轨迹
,求轨迹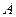 ,使点
,使点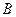
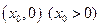 的最小距离不小于
的最小距离不小于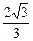 ,求实数
,求实数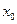 的取值范围.
的取值范围.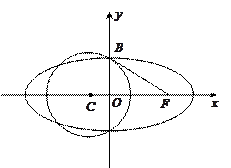
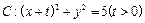 和椭圆
和椭圆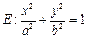
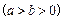 的一个公共点为
的一个公共点为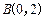 .
.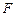 为椭圆
为椭圆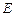 的右焦点,直线
的右焦点,直线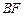 与圆
与圆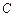 相切于点
相切于点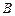 .
.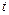 值和椭圆
值和椭圆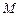 ,使
,使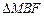 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点 过点
过点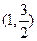 ,且长轴长等于4.
,且长轴长等于4.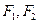 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若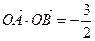 ,求
,求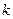 的值
的值
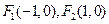 是椭圆的两个焦点,过
是椭圆的两个焦点,过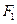 的直线
的直线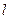 交椭圆于
交椭圆于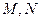 ,若
,若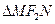 的周长为
的周长为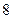 ,则椭圆方程为( ).
,则椭圆方程为( ).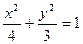
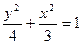
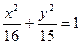
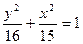
 分别是椭圆
分别是椭圆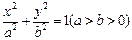 的上、下顶点和右焦点,直线
的上、下顶点和右焦点,直线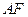 与椭圆的右准线交于点
与椭圆的右准线交于点 ,若直线
,若直线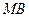 ∥
∥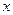 轴,则该椭圆的离心率
轴,则该椭圆的离心率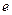 = ▲ .
= ▲ .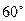 的菱形的四个顶点,则椭圆的离心率为 .
的菱形的四个顶点,则椭圆的离心率为 .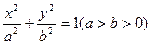 上存在一点M,它到左焦点的距离是它到右准线距离的2倍,则椭圆离心率的最小值为 .
上存在一点M,它到左焦点的距离是它到右准线距离的2倍,则椭圆离心率的最小值为 .