题目内容
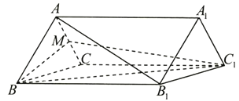
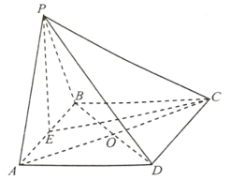
【题目】如图，四棱锥
的底面
是矩形，
，点
为
的中点，
与
交于点
.
（Ⅰ）求异面直线
与
所成角的余弦值；
（Ⅱ）求证：
；
（Ⅲ）求直线
与平面
所成角的正弦值.
【答案】（Ⅰ）
（Ⅱ）见证明；（Ⅲ）
【解析】
（I）根据
判断出
是异面直线成角，判断三角形
是直角三角形后，直接计算出线线角的余弦值.（II）先证得
,然后证得
，由此证得
平面
，从而证得平面
平面.（III）过点
作
与
的延长线交于点
，证得
直线
与平面
所成角，在
中，求得线面角的正弦值.
解：（Ⅰ）∵是矩形，∴
∴是异面直线成角
在
中，
∴在
中，
∴异面直线成角余弦值为
.
（Ⅱ）∵
，点
为
的中点∴
，又∵
∴
又∵
，∴
又∵
∴
（Ⅲ）过点作与的延长线交于点，
∵
，
为斜线在面内的射影
∴直线与平面所成角
在中，
∴
∴直线与平面所成角的正弦值
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
【题目】为增强市民的环境保护意识，某市面向全市学校征召100名教师做义务宣传志愿者，成立环境保护宣传组，现把该组的成员按年龄分成5组，如下表所示：
组别 | 年龄 | 人数 |
1 |
| 5 |
2 |
| 35 |
3 |
| 20 |
4 |
| 30 |
5 |
| 10 |
（Ⅰ）若从第3，4，5组中用分层抽样的方法选出6名志愿者参加某社区宣传活动，应从第3，4，5组各选出多少名志愿者？
（Ⅱ）在Ⅰ的条件下，宣传组决定在这6名志愿者中随机选2名志愿者介绍宣传经验.
（ⅰ）列出所有可能结果；
（ⅱ）求第4组至少有1名志愿者被选中的概率。
【题目】“微信运动”已经成为当下最热门的健身方式，小李的微信朋友圈内也有大量的好友参加了“微信运动”.他随机的选取了其中30人，记录了他们某一天走路的步数，将数据整理如下：
步数 |
|
|
|
人数 | 5 | 13 | 12 |
（1）若采用样本估计总体的方式，试估计小李所有微信好友中每日走路步数超过5000步的概率；
（2）已知某人一天的走路步数若超过8000步则他被系统评定为“积极型”，否则评定为“懈怠型”，将这30人按照“积极型”、“懈怠型”分成两层，进行分层抽样，从中抽取5人，将这5人中属于“积极型”的人依次记为
，属于“懈怠型”的人依次记为
，现再从这5人中随机抽取2人接受问卷调查.设
为事件“抽取的2人来自不同的类型”，求事件发生的概率.
【题目】从某地区随机抽测120名成年女子的血清总蛋白含量（单位：
），由测量结果得如图频数分布表：
（1）①仔细观察表中数据，算出该样本平均数
______；
②由表格可以认为，该地区成年女子的血清总蛋白含量Z服从正态分布
.其中
近似为样本平均数
，
近似为样本标准差s.经计算，该样本标准差
.
医学上，Z过高或过低都为异常，Z的正常值范围通常取关于对称的区间
，且Z位于该区间的概率为
，试用该样本估计该地区血清总蛋白正常值范围.
120名成年女人的血清总蛋白含量的频数分布表 | |||
分组 | 频数f | 区间中点值x |
|
| 2 | 65 | 130 |
| 8 | 67 | 536 |
| 12 | 69 | 828 |
| 15 | 71 | 1065 |
| 25 | 73 | 1825 |
| 24 | 75 | 1800 |
| 16 | 77 | 1232 |
| 10 | 79 | 790 |
| 7 | 81 | 567 |
| 1 | 83 | 83 |
合计 | 120 | 8856 | |
（2）结合（1）中的正常值范围，若该地区有5名成年女子检测血清总蛋白含量，测得数据分别为83.2，80，73，59.5，77，从中随机抽取2名女子，设血清总蛋白含量不在正常值范围的人数为X，求X的分布列和数学期望.
附：若
，则
.
