题目内容
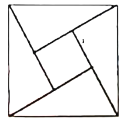
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为3个单位)的顶点
(边长为3个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A.21种B.24种C.25种D.27种
【答案】C
【解析】
抛掷三次骰子后棋子恰好又回到点![]() 处表示三次骰子的点数之和是12,列举出在点数中三个数字能够使得和为12的1,5,6;2,4,6;3,3,6;5,5,2;4,4,4,共有4种组合,前四种组合又可以排列出
处表示三次骰子的点数之和是12,列举出在点数中三个数字能够使得和为12的1,5,6;2,4,6;3,3,6;5,5,2;4,4,4,共有4种组合,前四种组合又可以排列出![]() 种结果,由此利用分类计数原理能得到结果.
种结果,由此利用分类计数原理能得到结果.
由题意知正方形![]() (边长为3个单位)的周长是12,
(边长为3个单位)的周长是12,
抛掷三次骰子后棋子恰好又回到点![]() 处表示三次骰子的点数之和是12,
处表示三次骰子的点数之和是12,
列举出在点数中三个数字能够使得和为12的有1,5,6;2,4,6;3,4,5;3,3,6;5,5,2;4,4,4;共有6种组合,
前三种组合1,5,6;2,4,6;3,4,5;又可以排列出![]() 种结果,
种结果,
3,3,6;5,5,2;有6种结果,4,4,4;有1种结果.
根据分类计数原理知共有![]() 种结果,
种结果,
故选:C.

【题目】为了了解手机品牌的选择是否和年龄的大小有关,随机抽取部分华为手机使用者和苹果机使用者进行统计,统计结果如下表:
年龄 手机品牌 | 华为 | 苹果 | 合计 |
30岁以上 | 40 | 20 | 60 |
30岁以下(含30岁) | 15 | 25 | 40 |
合计 | 55 | 45 | 100 |
附:
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
根据表格计算得![]() 的观测值
的观测值![]() ,据此判断下列结论正确的是( )
,据此判断下列结论正确的是( )
A.没有任何把握认为“手机品牌的选择与年龄大小有关”
B.可以在犯错误的概率不超过0.001的前提下认为“手机品牌的选择与年龄大小有关”
C.可以在犯错误的概率不超过0.01的前提下认为“手机品牌的选择与年龄大小有关”
D.可以在犯错误的概率不超过0.01