题目内容
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试，每位同学彼此独立的从
四所高校中选2所.
（1）求甲、乙、丙三名同学都选
高校的概率；
（2）若甲必选
，记
为甲、乙、丙三名同学中选校的人数，求随机变量的分布列及数学期望.
【答案】（1）
；（2）
.
【解析】
（1）利用组合知识，由古典概型概率公式可得结果；（2）求出甲同学选中
高校的概率与乙、丙同学选中高校的概率，判断
所有可能的取值为0,1,2,3，根据互斥事件的概率公式与独立事件概率公式求出各随机变量对应的概率，从而可得分布列，进而利用期望公式可得的数学期望.
（1）设“甲、乙、丙三名同学都选高校”为事件
，则
.
（2）甲同学选中高校的概率为：
，
乙、丙同学选中高校的概率为：
，
所有可能的取值为0,1,2,3，
，有
；
；
；
;
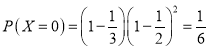的分布列为
| 0 | 1 | 2 | 3 |
| | | | |
.
【题目】某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在[29.94，30.06）的零件为优质品.从两个分厂生产的零件中各抽出了500件，量其内径尺寸，得结果如下表：
甲厂：
分组 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂：
分组 | [29.86，29.90） | [29.90，29.94） | [29.94，29.98） | [29.98，30.02） | [30.02，30.06） | [30.06，30.10） | [30.10，30.14） |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
（1）试分别估计两个分厂生产的零件的优质品率；
（2）由以上统计数据填下面
列联表，并问是否有
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附： 
|
|
|
|
|
|
|
|
|
|
【题目】光伏发电是利用太阳能电池及相关设备将太阳光能直接转化为电能，近几年在国内出台的光伏发电补贴政策的引导下，某地光伏发电装机量急剧上涨，如下表：
年份 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
新增光伏装机量 | 0.4 | 0.8 | 1.6 | 3.1 | 6.1 | 7.1 | 9.7 | 12.2 |
某位同学分别用两种模型：①
，②
进行拟合，得到相应的回归方程并进行残差分析，残差图如下（注：残差等于
）
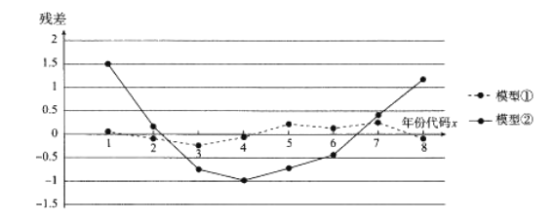
经过计算得
，
，
，
，其中
，
.
（1）根据残差图，比较模型①，②的拟合效果，应该选择哪个模型？并简要说明理由.
（2）根据（1）的判断结果及表中数据建立
关于
的回归方程，并预测该地区2020年新增光伏装机量是多少.（在计算回归系数时精确到0.01）
附：归直线的斜率和截距的最小二乘估计公式分别为：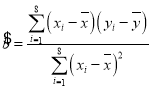
，
.