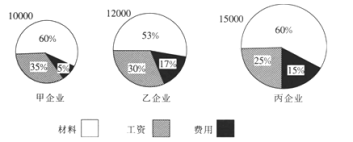
题目内容
【题目】为增强市民的环境保护意识,某市面向全市学校征召100名教师做义务宣传志愿者,成立环境保护宣传组,现把该组的成员按年龄分成5组,如下表所示:
组别 | 年龄 | 人数 |
1 |
| 5 |
2 |
| 35 |
3 |
| 20 |
4 |
| 30 |
5 |
| 10 |
(Ⅰ)若从第3,4,5组中用分层抽样的方法选出6名志愿者参加某社区宣传活动,应从第3,4,5组各选出多少名志愿者?
(Ⅱ)在Ⅰ的条件下,宣传组决定在这6名志愿者中随机选2名志愿者介绍宣传经验.
(ⅰ)列出所有可能结果;
(ⅱ)求第4组至少有1名志愿者被选中的概率。
【答案】(Ⅰ )2,3,1(Ⅱ)(i)见解析(ii)![]()
【解析】
(Ⅰ )根据抽样比即可得到结果;(Ⅱ)(ⅰ)利用列举法得到所有可能结果;
(ⅱ)利用对立事件概率公式得到结果.
(Ⅰ )从第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,
由频率分布图得:
应从第3组抽取:6![]() 2名志愿者,
2名志愿者,
应从第4组抽取:6![]() 3名志愿者,
3名志愿者,
应从第5组抽取:6![]() 1名志愿者.
1名志愿者.
(Ⅱ)(ⅰ)记第3组的2名志愿者为A1,A2,第4组的3名志愿者为B1,B2,B3第5组的1名志愿者为C1.
则从6名志愿者中抽取2名志愿者有:
(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,C1),
(A2,B1),(A2,B2),(A2,B3),(A2,C1),
(B1,B2),(B1,B3),(B1,C1),
(B2,B3)(B2,C1),
(B3,C1),
共有15种.
(ⅱ)第4组没有志愿者被选中包括(A1,A2),(A1,C1),(A2,C1),共三种,
故第4组至少有1名志愿者被选中的概率![]()

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
| ① | ② |
| 0.050 | |
| 0.200 | |
| 12 | 0.300 |
| 0.275 | |
| 0.050 | |
合计 | ④ |
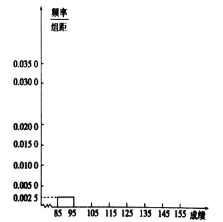
(1)根据上面图表,①②④处的数值分别为______,______,______;
(2)在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.