题目内容
【题目】(本小题满分13分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
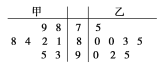
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
【答案】(1)见解析;(2)甲.
【解析】
试题
(1)根据所给的两组数据,用十位做茎,个位做叶,写出茎叶图,根据乙组数据有8个数字,这组数据的中位数是最中间两个数的平均数,乙组数据的中位数为85.
(2)根据所给的两组数据,分别求出两组数据的平均数,再求出两组数据的方差,比较所得的两组结果,甲和乙的平均数相同,甲的方差较小,成绩比较稳定.
试题解析: (1)作出茎叶图如下:
(2)由题意可得:
![]() =
=![]() (78+79+81+82+84+88+93+95)=85,
(78+79+81+82+84+88+93+95)=85,
![]() =
=![]() (75+80+80+83+85+90+92+95)=85.
(75+80+80+83+85+90+92+95)=85.
所以![]() =
=![]() [(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
![]() =
=![]() [(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
∵![]() =
=![]() ,
, ![]() <
<![]() ∴甲的成绩较稳定,派甲参赛比较合适.
∴甲的成绩较稳定,派甲参赛比较合适.

【题目】某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在表中,如何设计甲、乙两种货物应各托运的箱数可以获得最大利润,最大利润是多少?
货物 | 体积 | 重量 | 利润 |
甲 | 5 | 2 | 20 |
乙 | 4 | 5 | 10 |
托运限制 | 24 | 13 |
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.