题目内容
【题目】如图,已知椭圆C: ![]() ,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
,点A,B分别是左、右顶点,过右焦点F的直线MN(异于x轴)交于椭圆C于M、N两点.
(1)若椭圆C过点 ,且右准线方程为
,且右准线方程为![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)若直线BN的斜率是直线AM斜率的2倍,求椭圆C的离心率.

【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据曲线上的点和右准线方程写出椭圆方程;(2)设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ;因为点
;因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,所以
,所以![]() ,联立方程消元,根据韦达定理可得
,联立方程消元,根据韦达定理可得 ,又
,又![]() ,进而求得离心率.
,进而求得离心率.
试题解析:(1)因为椭圆![]() 过点
过点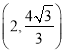 ,所以
,所以![]() ,
,
又已知右准线方程为![]() ,所以
,所以![]() ,
, ![]() ,
,
可解得![]() ,
, ![]() ;或
;或![]() ,
, ![]() ;
;
所以椭圆![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ;
;
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以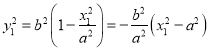 ,
,
所以![]() ,
,
设直线![]() :
: ![]() ,与椭圆
,与椭圆![]() :
: ![]() 联立方程组消去
联立方程组消去![]() 得
得
![]() ,
,
![]()
![]() ,
,
将![]() ,
, ![]() 代入上式化简得
代入上式化简得
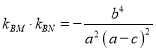 ,又
,又![]() ;所以
;所以 ,
,
得![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,即椭圆
,即椭圆![]() 的离心率为
的离心率为![]() .
.
点睛:本题考查直线与抛物线的位置关系的问题,其中过焦点的最短弦长为通径. 直线与圆锥曲线的位置关系从几何角度看:当直线与双曲线的渐进线平行时,直线与双曲线只有一个交点;当直线与抛物线的对称轴平行或重合时,直线与抛物线也只有一个交点.从代数角度看:设直线L的方程与圆锥曲线的方程联立得到![]() .若
.若![]() =0,当圆锥曲线是双曲线时,直线L与双曲线的渐进线平行或重合;当圆锥曲线是抛物线时,直线L与抛物线的对称轴平行或重合.若
=0,当圆锥曲线是双曲线时,直线L与双曲线的渐进线平行或重合;当圆锥曲线是抛物线时,直线L与抛物线的对称轴平行或重合.若![]() ,设
,设![]() .
. ![]() 时,直线和圆锥曲线相交于不同两点,相交.
时,直线和圆锥曲线相交于不同两点,相交. ![]() 时,直线和圆锥曲线相切于一点,相切.
时,直线和圆锥曲线相切于一点,相切. ![]() 时,直线和圆锥曲线没有公共点,相离.
时,直线和圆锥曲线没有公共点,相离.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目