题目内容
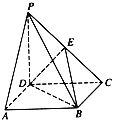
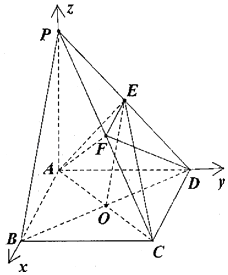
【题目】如图,四棱锥P﹣ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点. (Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形, ![]() ,求二面角C﹣AF﹣D大小.
,求二面角C﹣AF﹣D大小.
【答案】证明:(Ⅰ)连接BD,设AC∩BD=O,连结OE,
∵四边形ABCD为矩形,∴O是BD的中点,
∵点E是棱PD的中点,∴PB∥EO,
又PB平面AEC,EO平面AEC,
∴PB∥平面AEC.
(Ⅱ)由题可知AB,AD,AP两两垂直,
分别以 ![]() 、
、 ![]() 、
、 ![]() 的方向为坐标轴方向建立空间直角坐标系.
的方向为坐标轴方向建立空间直角坐标系.
设由 ![]() 可得AP=AB,
可得AP=AB,
于是可令AP=AB=AD=2,则
A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,1,1),F(1,1,1)
设平面CAF的一个法向量为 ![]() .由于
.由于 ![]() ,
,
∴ ![]() ,解得x=﹣1,所以
,解得x=﹣1,所以 ![]() .
.
∵y轴平面DAF,∴设平面DAF的一个法向量为 ![]() .
.
∵ ![]() ,∴
,∴ ![]() ,解得z=﹣1,
,解得z=﹣1,
∴ ![]() .
.
∴  .∴二面角C﹣AF﹣D的大小为60°.
.∴二面角C﹣AF﹣D的大小为60°.
【解析】(Ⅰ)连接BD,设AC∩BD=O,连结OE,推导出PB∥EO,由此能证明PB∥平面AEC.(Ⅱ)分别以 ![]() 、
、 ![]() 、
、 ![]() 的方向为坐标轴方向建立空间直角坐标系,利用向量法能求出二面角C﹣AF﹣D的大小.
的方向为坐标轴方向建立空间直角坐标系,利用向量法能求出二面角C﹣AF﹣D的大小.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目