题目内容
已知数列{an}的通项公式是an=n2+kn+2,若对于n∈N*,都有an+1>an成立,则实数的取值范围( )
| A.k>0 | B.k>﹣1 | C.k>﹣2 | D.k>﹣3 |
D
∵对于n∈N*,都有an+1>an成立,
∴(n+1)2+k(n+1)+2>n2+kn+2,化为k>﹣(2n+1),
∴k>﹣(2×1+1),即k>﹣3.
故选D.
∴(n+1)2+k(n+1)+2>n2+kn+2,化为k>﹣(2n+1),
∴k>﹣(2×1+1),即k>﹣3.
故选D.

练习册系列答案
相关题目
 为单调递增的等比数列,且
为单调递增的等比数列,且 ,
, ,
, 是首项为2,公差为
是首项为2,公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
. ,
, ,
, 成立,求
成立,求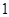 的等比数列
的等比数列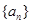 的首项
的首项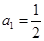 ,前
,前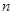 项和为
项和为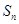 ,且
,且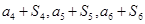 成等差数列.
成等差数列.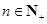 ,在
,在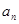 与
与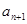 之间插入
之间插入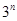 个数,使这
个数,使这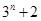 个数成等差数列,记插入的这
个数成等差数列,记插入的这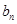 ,求数列
,求数列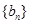 的前
的前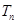 .
.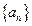 是首项为
是首项为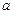 ,公差为
,公差为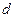 的等差数列(d≠0),
的等差数列(d≠0),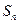 是其前
是其前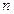 项和.记bn=
项和.记bn=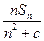 ,
,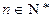 ,其中
,其中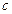 为实数.
为实数. ,且
,且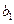 ,
,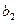 ,
,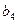 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+);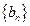 是等差数列,证明:
是等差数列,证明: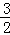 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.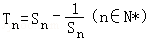 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值. 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( ).
( ).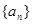 满足
满足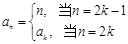 ,其中
,其中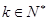 ,设
,设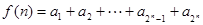 ,则
,则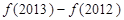 等于( )
等于( )


