题目内容
已知椭圆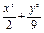 =1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
=1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且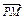 =2
=2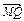 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足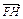 =2
=2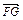 ,求直线l的方程.
,求直线l的方程.
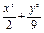 =1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
=1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且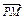 =2
=2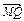 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.(1)求曲线E的方程;
(2)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足
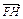 =2
=2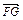 ,求直线l的方程.
,求直线l的方程.(1) +y2=1(2)y=±
+y2=1(2)y=± x+2
x+2
 +y2=1(2)y=±
+y2=1(2)y=± x+2
x+2(1)设M(x,y),P(x0,y0),
∵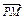 =2
=2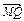 ,∴
,∴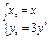
将其代入椭圆方程得 =1
=1
得曲线E的方程为: +y2="1."
+y2="1."
(2)设G(x1,y1)、H(x2,y2),
∵ =2
=2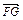 ,∴x2=2x1 ①
,∴x2=2x1 ①
依题意,当直线l斜率不存在时,G(0,1),H(0,-1),不满足 =2
=2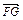 .故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6="0, " (*)
.故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6="0, " (*)
∴x1+x2=-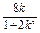 ,x1·x2=
,x1·x2= ②
②
联立①②解得k=± ,此时(*)中Δ>0.
,此时(*)中Δ>0.
所以直线l的方程为:y=± x+2.
x+2.
∵
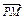 =2
=2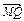 ,∴
,∴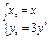
将其代入椭圆方程得
 =1
=1得曲线E的方程为:
 +y2="1."
+y2="1." (2)设G(x1,y1)、H(x2,y2),
∵
 =2
=2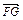 ,∴x2=2x1 ①
,∴x2=2x1 ①依题意,当直线l斜率不存在时,G(0,1),H(0,-1),不满足
 =2
=2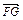 .故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6="0, " (*)
.故设直线l:y=kx+2,代入曲线E的方程并整理得(1+2k2)x2+8kx+6="0, " (*)∴x1+x2=-
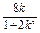 ,x1·x2=
,x1·x2= ②
②联立①②解得k=±
 ,此时(*)中Δ>0.
,此时(*)中Δ>0.所以直线l的方程为:y=±
 x+2.
x+2.
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 之间满足
之间满足
 ,求b的值
,求b的值 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值; ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使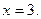 (I)求椭圆C的方程; (II)过点F作斜率为k的直线l,与椭圆C交于A、B两点,若
(I)求椭圆C的方程; (II)过点F作斜率为k的直线l,与椭圆C交于A、B两点,若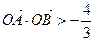 ,求k的取值范围。
,求k的取值范围。 的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.  ,一个焦点是F(-m,0)(m是大于0的常数).
,一个焦点是F(-m,0)(m是大于0的常数). |=2|
|=2| |,求直线l的斜率.
|,求直线l的斜率.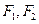 是椭圆
是椭圆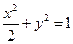 的两个焦点,过
的两个焦点,过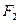 作倾斜角为
作倾斜角为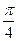 的弦
的弦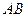 ,得
,得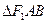 ,求
,求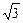 ),椭圆
),椭圆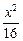 +
+ 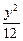 =1的右焦点为F,点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少?
=1的右焦点为F,点P在椭圆上移动.当|PA|+2|PF|取最小值时,P点的坐标是多少? 的内部,则m的取值范围是 ( )
的内部,则m的取值范围是 ( ) <m<
<m<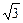 ,求这个椭圆方程.
,求这个椭圆方程.