题目内容
椭圆 的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
 的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.
的右焦点为F,P1,P2,…,P24为24个依逆时针顺序排列在椭圆上的点,其中P1是椭圆的右顶点,并且∠P1FP2=∠P2FP3=∠P3FP4=…=∠P24FP1.若这24个点到右准线的距离的倒数和为S,求S2的值.  180
180椭圆中,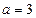 ,
,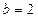 ,故
,故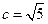 .所以
.所以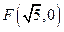 ,
,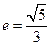 .
.
设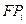 与
与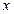 轴正向的夹角为
轴正向的夹角为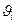 ,
, 为点
为点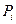 到右准线的距离.则
到右准线的距离.则
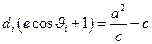 .即
.即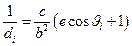 .
.
同理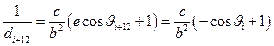 .
.
所以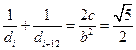 .
.
从而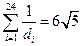 ,于是
,于是 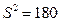 .
.
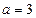 ,
,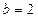 ,故
,故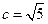 .所以
.所以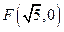 ,
,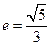 .
.设
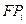 与
与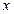 轴正向的夹角为
轴正向的夹角为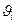 ,
, 为点
为点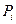 到右准线的距离.则
到右准线的距离.则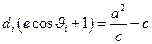 .即
.即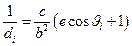 .
. 同理
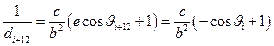 .
.所以
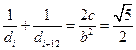 .
.从而
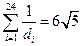 ,于是
,于是 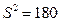 .
.
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 =1表示焦点在y轴上的椭圆,求实数m的取值范围.
=1表示焦点在y轴上的椭圆,求实数m的取值范围.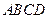 中,
中,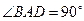 ,
,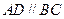 ,
,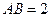 ,
,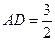 ,
,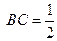 ,椭圆以
,椭圆以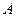 、
、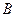 为焦点且经过点
为焦点且经过点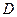 .
.
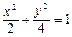 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足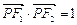 ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点. 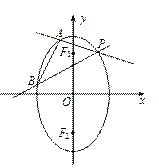
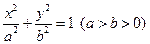 , 线段
, 线段 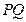 是过左焦点
是过左焦点 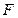 且不与
且不与 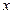 轴垂直的焦点弦. 若在左准线上存在点
轴垂直的焦点弦. 若在左准线上存在点 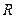 , 使
, 使 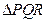 为正三角形, 求椭圆的离心率
为正三角形, 求椭圆的离心率 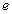 的取值范围, 并用
的取值范围, 并用 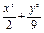 =1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且
=1上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且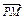 =2
=2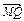 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.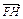 =2
=2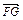 ,求直线l的方程.
,求直线l的方程. (a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3两段,则此椭圆的离心率为( )



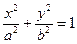 (a>b>0)的一个焦点且垂直于x轴的直线与椭圆C交于点(
(a>b>0)的一个焦点且垂直于x轴的直线与椭圆C交于点(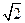 ,1).(1)求椭圆C的方程;(2)设过点P(4,1)的动直线
,1).(1)求椭圆C的方程;(2)设过点P(4,1)的动直线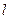 与椭圆C相交于两个不同点A、B,与直线2x+y-2=0交于点Q,若
与椭圆C相交于两个不同点A、B,与直线2x+y-2=0交于点Q,若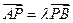 ,
,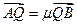 ,求λ+μ的值
,求λ+μ的值