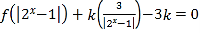Question

【题目】求下列方程组的解集：

（1）（2）

Answer 1

【答案】（1）；（2）.

【解析】

（1）方法一：由得出，代入，利用代入消元法可求出原方程组的解集；

方法二：根据一元二次方程根与系数的关系，可将、视为关于的一元二次方程的两个实数解，解出该方程，即可得出原方程组的解集；

（2）根据一元二次方程根与系数的关系，可将、视为关于的一元二次方程的两根，解出这个方程，可求出、的值，即可得出原方程组的解集.

（1）方法一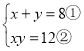：，由①得，③，

把③代入②，整理得，解得或，

把代入③得，把代入③得，

因此，原方程组的解集是；

方法二：根据一元二次方程根与系数的关系可知，

则、是关于的一元二次方程的两个实数解，

解这个方程得，，因此，原方程组的解集是；

（2），

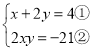方程①是与的和，方程②是与的积，

与是关于的一元二次方程的两根，

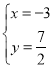解此方程得，，或，解得或.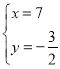

因此，原方程组的解集是.