题目内容
【题目】已知数列![]() (其中第一项是
(其中第一项是![]() ,接下来的
,接下来的![]() 项是
项是![]() ,再接下来的
,再接下来的![]() 项是
项是![]() ,依此类推)的前
,依此类推)的前![]() 项和为
项和为![]() ,下列判断:
,下列判断:
①![]() 是
是![]() 的第
的第![]() 项;②存在常数
项;②存在常数![]() ,使得
,使得![]() 恒成立;③
恒成立;③![]() ;④满足不等式
;④满足不等式![]() 的正整数
的正整数![]() 的最小值是
的最小值是![]() .
.
其中正确的序号是( )
A.①③B.①④C.①③④D.②③④
【答案】B
【解析】
找出数列![]() 的规律:分母为
的规律:分母为![]() 的项有
的项有![]() 项,并将这些项排成杨辉三角形式的数阵,使得第
项,并将这些项排成杨辉三角形式的数阵,使得第![]() 有
有![]() 项,每项的分母均为
项,每项的分母均为![]() ,并计算出每行各项之和
,并计算出每行各项之和![]() ,并计算出数列
,并计算出数列![]() 的前
的前![]() 项和
项和![]() ,结合这些规律来判断各题的正误。
,结合这些规律来判断各题的正误。
由题意可知,数列![]() 的规律为:分母为
的规律为:分母为![]() 的项有
的项有![]() 项,将数列
项,将数列![]() 中的项排成杨辉三角数阵,且使得第
中的项排成杨辉三角数阵,且使得第![]() 行每项的分母为
行每项的分母为![]() ,该行有
,该行有![]() 项,如下所示:
项,如下所示:
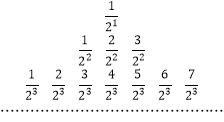
对于命题①,![]() 位于数阵第
位于数阵第![]() 行最后一项,对应于数列
行最后一项,对应于数列![]() 的项数为
的项数为
![]() ,命题①正确;
,命题①正确;
对于命题②,数阵中第![]() 行各项之和为
行各项之和为![]() ,则
,则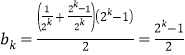 ,
,
且数列![]() 的前
的前![]() 项之和为
项之和为
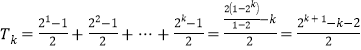 ,
,
当![]() 时,
时,![]() ,因此,不存在正数
,因此,不存在正数![]() ,使得
,使得![]() ,命题②错误;
,命题②错误;
对于命题③,易知第![]() 行最后一项位于数列
行最后一项位于数列![]() 的项数为
的项数为
![]() ,
,
第![]() 行最后一项位于数列
行最后一项位于数列![]() 的项数为
的项数为![]() ,且
,且![]() ,
,
则![]() 位于数阵第
位于数阵第![]() 行第
行第![]() 项(即
项(即![]() ),
),
所以,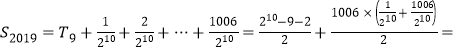
![]() ,命题③错误;
,命题③错误;
由①知,![]() ,且
,且![]() ,
,
则恰好满足![]() 的项
的项![]() 位于第
位于第![]() 行,假设位于第
行,假设位于第![]() 项,
项,
则有![]() ,可得出
,可得出![]() ,
,
由于![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
因此,满足![]() 的最小正整数
的最小正整数![]() ,命题④正确。
,命题④正确。
故选:B.

练习册系列答案
相关题目